

分析 (1)先求出点A坐标,求出直线AD的解析式,利用方程组求出点E坐标,利用两点间距离公式即可解决问题.
(2)构建二次函数,求出d最大时点P坐标,作EM⊥PQ交PQ的延长线于M,作KN⊥EM于N.只要证明PM就是PK+$\frac{1}{2}$EK的最小值即可解决问题.
(3)分四种情形①如图2中,当Q′Q=AQ′时,∠Q′PQ=∠Q′PA=30°,∠NPE=∠NPQ′=15°,连接PA,在PF上取一点E,使得PE=EN.设FN=x,则PE=EN=2x,EF=$\sqrt{3}$x,列出方程求解即可.②如图3中,当N与A重合时△AQQ′是等腰三角形.此时N($\sqrt{3}$,0).③如图4中,当N与B重合时,△AQQ′是等腰三角形,此时N(-3$\sqrt{3}$,0).④如图5中,当Q′Q=Q′A,易知∠PNF=∠PQQ′=∠PQ′Q=15°,在FN上取一点E,使得PE=BE.在Rt△PEF中解直角三角形即可解决问题.
解答 解:(1)对于抛物线y=-$\frac{1}{3}$x2-$\frac{2\sqrt{3}}{3}$x+3,
令y=0,得-$\frac{1}{3}$x2-$\frac{2\sqrt{3}}{3}$x+3=0,解得x=-3$\sqrt{3}$或$\sqrt{3}$,
∴A($\sqrt{3}$,0),B(-3$\sqrt{3}$,0),
∵D(0,-1),
设直线AD的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-1}\\{\sqrt{3}k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-1}\end{array}\right.$,
∴直线AD的解析式为y=$\frac{\sqrt{3}}{3}$x-1.
由$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x-1}\\{y=-\frac{1}{3}{x}^{2}-\frac{2\sqrt{3}}{3}x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4\sqrt{3}}\\{y=-5}\end{array}\right.$,
∴点E坐标为(-4$\sqrt{3}$,-5),
∴DE=$\sqrt{(4\sqrt{3})^{2}+{4}^{2}}$=8.
(2)如图1中,设P(m,-$\frac{1}{3}$m2-$\frac{2\sqrt{3}}{3}$m+3)则Q(m,$\frac{\sqrt{3}}{3}$m-1).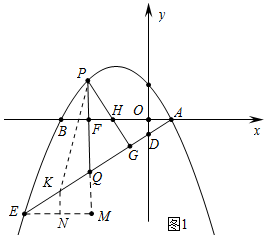
∵tan∠OAD=$\frac{DO}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠OAD=30°,
∵PG⊥AE,
∴∠AGH=90°,
∴∠AHG=∠PHF=60°,
∴PH=$\frac{PF}{cos60°}$,
∴d=PQ-$\frac{\sqrt{3}}{4}$PH=-$\frac{1}{3}$m2-$\sqrt{3}$m+4-$\frac{\sqrt{3}}{4}$×$\frac{2}{\sqrt{3}}$(-$\frac{1}{3}$m2-$\frac{2\sqrt{3}}{3}$m+3)=-$\frac{1}{6}$(m+2$\sqrt{3}$)2+$\frac{9}{2}$,
∵-$\frac{1}{6}$<0,
∴m=-2$\sqrt{3}$时,d的值最大,P(-2$\sqrt{3}$,3),
作EM⊥PQ交PQ的延长线于M,作KN⊥EM于N.
∵∠AEM=∠OAD=30°,
∴KN=$\frac{1}{2}$EK,QM=$\frac{1}{2}$EQ,
∴PK+$\frac{1}{2}$EK=PK+KN≤PM,
∴当K与Q重合时,PK+$\frac{1}{2}$EK的值最小,
此时K(-2$\sqrt{3}$,-3),最小值为8.
(3)①如图2中,连接PA,在PF上取一点E,使得PE=EN.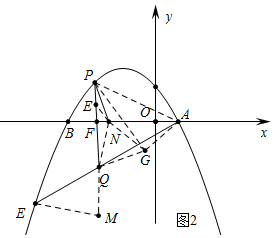
∵PF=3,AF=3$\sqrt{3}$,
∴tan∠AFP=$\frac{\sqrt{3}}{3}$,
∴∠PAF=30°,∠PAQ=60°,
∵PF=FQ,AF⊥PQ,
∴AP=AQ,
∴△PAQ是等边三角形,
当Q′Q=AQ′时,∠Q′PQ=∠Q′PA=30°,∠NPE=∠NPQ′=15°,
∴∠NEF=30°,设FN=x,则PE=EN=2x,EF=$\sqrt{3}$x,
∵PF=3,
∴2x+$\sqrt{3}$x=3,
∴x=6-3$\sqrt{3}$,
∴OF=2$\sqrt{3}$-6+3$\sqrt{3}$=5$\sqrt{3}$-6,
∴N(6-5$\sqrt{3}$,0).
②如图3中,当N与A重合时△AQQ′是等腰三角形.此时N($\sqrt{3}$,0).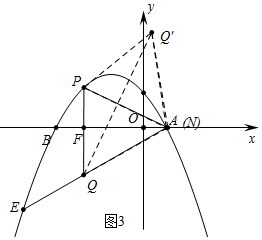
③如图4中,当N与B重合时,△AQQ′是等腰三角形,此时N(-3$\sqrt{3}$,0).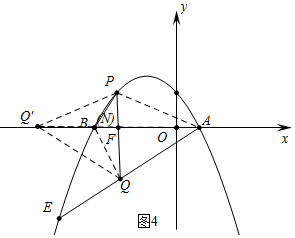
④如图5中,当Q′Q=Q′A,易知∠PNF=∠PQQ′=∠PQ′Q=15°,在FN上取一点E,使得PE=BE.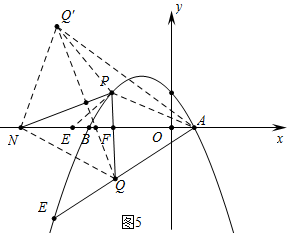
在Rt△PEF中,∵PF=3,∠PEF=30°,
∴PE=NE=2PF=6,EF=$\sqrt{3}$PF=3$\sqrt{3}$,
∴ON=6+5$\sqrt{3}$,
∴N(-6-5$\sqrt{3}$,0).
综上所述,满足条件的点N坐标为(6-5$\sqrt{3}$,0)或($\sqrt{3}$,0)或(-3$\sqrt{3}$,0)或(-6-5$\sqrt{3}$,0).
点评 本题考查二次函数综合题、一次函数、等边三角形的判定和性质、最小值问题等知识,解题的关键是学会构建二次函数解决最值问题,学会利用垂线段最短解决最短问题,学会分类讨论,注意不能漏解,题目比较难,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
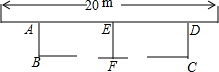 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com