
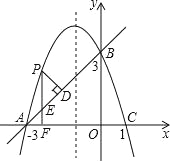
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)(﹣![]() ,
,![]() )
)
【解析】
(1)将A(-3,0),B(0,3),C(1,0)三点的坐标代入y=ax2+bx+c,运用待定系数法即可求出此抛物线的解析式;
(2)先证明△AOB是等腰直角三角形,得出∠BAO=45°,再证明△PDE是等腰直角三角形,则PE越大,△PDE的周长越大,再运用待定系数法求出直线AB的解析式为y=x+3,则可设P点的坐标为(x,-x2-2x+3),E点的坐标为(x,x+3),那么PE=(-x2-2x+3)-(x+3)=-(x+![]() )2+
)2+![]() ,根据二次函数的性质可知当x=-
,根据二次函数的性质可知当x=-![]() 时,PE最大,△PDE的周长也最大.将x=-
时,PE最大,△PDE的周长也最大.将x=-![]() 代入-x2-2x+3,进而得到P点的坐标.
代入-x2-2x+3,进而得到P点的坐标.
解:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0),
∴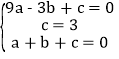 ,
,
解得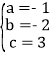 ,
,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)∵A(﹣3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°.
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PE越大,△PDE的周长越大.
设直线AB的解析式为y=kx+b,则
![]() ,解得
,解得![]() ,
,
即直线AB的解析式为y=x+3.
设P点的坐标为(x,﹣x2﹣2x+3),E点的坐标为(x,x+3),
则PE=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
所以当x=﹣![]() 时,PE最大,△PDE的周长也最大.
时,PE最大,△PDE的周长也最大.
当x=﹣![]() 时,﹣x2﹣2x+3=﹣(﹣
时,﹣x2﹣2x+3=﹣(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )+3=
)+3=![]() ,
,
即点P坐标为(﹣![]() ,
,![]() )时,△PDE的周长最大.
)时,△PDE的周长最大.


科目:初中数学 来源: 题型:
【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
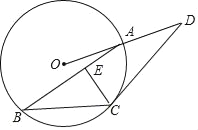
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省温州市)如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数![]() (k≠0)的图象恰好经过点A′,B,则k的值为______.
(k≠0)的图象恰好经过点A′,B,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
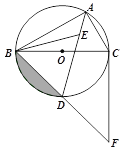
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD![]() DF,连接CF、BE.
DF,连接CF、BE.
(1)求证:DB![]() DE;
DE;
(2)求证:直线CF为⊙O的切线;
(3)若CF![]() 4,求图中阴影部分的面积.
4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 、图
、图![]() 、图
、图![]() ,在矩形
,在矩形![]() 中,
中,![]() 是
是![]() 边上的一点,以
边上的一点,以![]() 为边作平行四边形
为边作平行四边形![]() ,使点
,使点![]() 在
在![]() 的对边
的对边![]() 上,
上,
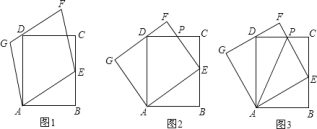
![]() 如图
如图![]() ,试说明:平行四边形
,试说明:平行四边形![]() 的面积与矩形
的面积与矩形![]() 的面积相等;
的面积相等;
![]() 如图
如图![]() ,若平行四边形
,若平行四边形![]() 是矩形,
是矩形,![]() 与
与![]() 交于点
交于点![]() ,试说明:
,试说明:![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上;
四点在同一个圆上;
![]() 如图
如图![]() ,若
,若![]() ,平行四边形
,平行四边形![]() 是正方形,且
是正方形,且![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,判断以
,判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b(a≠0)与y轴交与点C,与双曲线y=![]() (m≠0)交于A、B两点,AD⊥y轴于点D,连接BD,已知OC=AD=2,cos∠ACD=
(m≠0)交于A、B两点,AD⊥y轴于点D,连接BD,已知OC=AD=2,cos∠ACD=![]() .
.
(1)求直线AB和双曲线的解析式.
(2)求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但每件进价贵了4元,结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元,且两批玩具全部售完.
(1)第一次购进了多少件玩具?
(2)求该玩具店销售这两批玩具共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com