
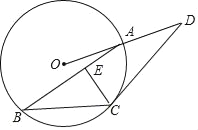
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
【答案】(1)∠D=32°;(2)①BE=![]() ;②
;②![]()
【解析】
(Ⅰ)连接OC, CD为切线,根据切线的性质可得∠OCD=90°,根据圆周角定理可得∠AOC=2∠ABC=29°×2=58°,根据直角三角形的性质可得∠D的大小.
(Ⅱ)①根据∠D=30°,得到∠DOC=60°,根据∠BAO=15°,可以得出∠AOB=150°,进而证明△OBC为等腰直角三角形,根据等腰直角三角形的性质得出![]()
根据圆周角定理得出![]() 根据含
根据含![]() 角的直角三角形的性质即可求出BE的长;
角的直角三角形的性质即可求出BE的长;
②根据四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB进行计算即可.
(Ⅰ)连接OC,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠AOC=2∠ABC=29°×2=58°,
∴∠D=90°﹣58°=32°;
(Ⅱ)①连接OB,
在Rt△OCD中,∵∠D=30°,
∴∠DOC=60°,![]()
∵∠BAO=15°,
∴∠OBA=15°,
∴∠AOB=150°,
∴∠OBC=150°﹣60°=90°,
∴△OBC为等腰直角三角形,
∴![]()
∵![]()
在Rt△CBE中,![]()
∴![]()
②作BH⊥OA于H,如图,
∵∠BOH=180°﹣∠AOB=30°,
∴![]()
∴四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB
![]()


科目:初中数学 来源: 题型:
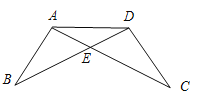
【题目】在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)上述四个条件中,由哪两个条件可以判定![]() 是等腰三角形?用序号写出所有成立的情形.
是等腰三角形?用序号写出所有成立的情形.
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 网格中,每个小正方形的边长都为
网格中,每个小正方形的边长都为![]() .
.

(1)建立如图所示的平面直角坐标系,若点![]() ,则点
,则点![]() 的坐标_______________;
的坐标_______________;
(2)将![]() 向左平移
向左平移![]() 个单位,向上平移
个单位,向上平移![]() 个单位,则点
个单位,则点![]() 的坐标变为_____________;
的坐标变为_____________;
(3)若将![]() 的三个顶点的横纵坐标都乘以
的三个顶点的横纵坐标都乘以![]() ,请画出
,请画出![]() ;
;
(4)图中格点![]() 的面积是_________________;
的面积是_________________;
(5)在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小,请画出点
最小,请画出点![]() 的位置,并直接写出
的位置,并直接写出![]() 的最小值是______________.
的最小值是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①△DFP~△BPH;②![]() ;③PD2=PHCD;④
;③PD2=PHCD;④![]() ,其中正确的是______(写出所有正确结论的序号).
,其中正确的是______(写出所有正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
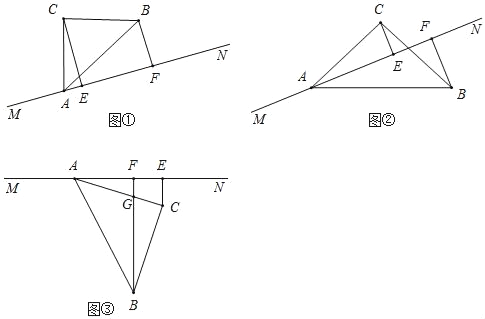
【题目】如图,在等腰直角△ABC中,∠C是直角,点A在直线MN上,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当C,B两点均在直线MN的上方时,
①直接写出线段AE,BF与CE的数量关系.
②猜测线段AF,BF与CE的数量关系,不必写出证明过程.
(2)将等腰直角△ABC绕着点A顺时针旋转至图2位置时,线段AF,BF与CE又有怎样的数量关系,请写出你的猜想,并写出证明过程.
(3)将等腰直角△ABC绕着点A继续旋转至图3位置时,BF与AC交于点G,若AF=3,BF=7,直接写出FG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
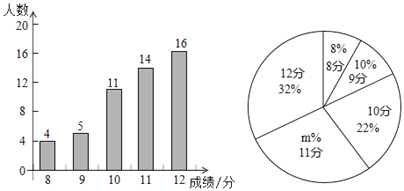
(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
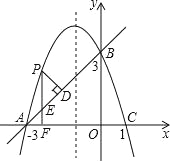
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=![]() x2+
x2+![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧)与y轴交于点C,直线BE⊥BC与点B,与抛物线的另一交点为E.
与x轴交于A、B两点(点A在点B的左侧)与y轴交于点C,直线BE⊥BC与点B,与抛物线的另一交点为E.
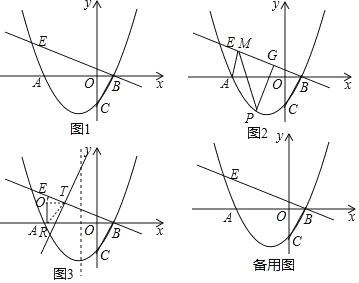
(1)如图1,求点E的坐标;
(2)如图2,若点P为x轴下方抛物线上一动点,过P作PG⊥BE与点G,当PG长度最大时,在直线BE上找一点M,使得△APM的周长最小,并求出周长的最小值.
(3)如图3,将△BOC在射线BE上,设平移后的三角形为△B′O′C′,B′在射线BE上,若直线B′C′分别与x轴、抛物线的对称轴交于点R、T,当△O′RT为等腰三角形时,求R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com