练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

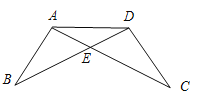
    【题目】在一次数学课上，王老师在黑板上画出一幅图，并写下了四个等式：

    ①，②，③，④．

    （1）上述四个条件中，由哪两个条件可以判定是等腰三角形？用序号写出所有成立的情形．

    （2）请选择(1)中的一种情形，写出证明过程．

    【答案】（1）①③、①④、②③、②④；（2）选择①③，证明见解析

    【解析】

    （1）只要能证明△ABE≌△DCE的条件都可以，所以可以根据全等三角形的判定方法来写出答案；

    （2）选择一种证明△ABE≌△DCE，可得到AE＝DE，可证明△AED为等腰三角形．

    （1）①③、①④、②③、②④都可以证明△ABE≌△DCE，可得到AE＝DE，可判定△AED为等腰三角形；

    （2）选择①③，证明如下：

    在△ABE和△DCE中，

    ，

    ∴△ABE≌△DCE（AAS），

    ∴AE＝DE，

    ∴△AED为等腰三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：一般地，个相同的因数相乘 ，记为．如，此时，叫做以为底的对数，记为（即）．一般地，若，（且，），则叫做以为底的对数，记为（即）．如，则叫做以为底的对数，记为（即）．

    （1）计算以下各对数的值：__________，__________，__________．

    （2）观察（1）中三数、，之间满足怎样的关系式，、、之间又满足怎样的关系式；

    （3）由（2）的结果，你能归纳出一个一般性的结论吗？__________．（且，，）

    （4）根据幂的运算法则：以及对数的含义证明上述结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】苏州太湖养殖场计划养殖蟹和贝类产品，这两个品种的种苗的总投放量只有50吨，根据经验测算，这两个品种的种苗每投放一吨的先期投资，养殖期间的投资以及产值如下表（单位：万元/吨）

    品种

    先期投资

    养殖期间投资

    产值

    贝类产品

    0.9

    0.3

    0.33

    蟹产品

    0.4

    1

    2

    养殖场受经济条件的影响，先期投资不超过36万元，养殖期间的投资不超过29万元，设贝类的种苗投放量为x吨，

    （1）求x的取值范围；

    （2）设这两个品种产出后的总产值为y（万元），试写出y与x之间的函数关系式，并求出当x等于多少时，y有最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

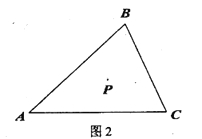
    【题目】P是三角形 内一点，射线PD//AC ，射线PB//AB .

    （1）当点D,E分别在AB,BC 上时，

    ①补全图1：

    ②猜想 与 的数量关系，并证明；，

    （2）当点都在线段上时，请先画出图形，想一想你在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中正确的是 ( )

    A. 在 Rt△ABC中，若tanA＝，则a＝4，b＝3

    B. 在 Rt△ABC中，∠C＝90°，则tanA＋tanB＝1

    C. 在 Rt△ABC 中，∠C＝90°，若a＝3，b＝4，则tanA＝

    D. tan75°＝tan(45°＋30°)＝tan45°＋tan30°＝1＋

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与坐标轴分别交于A（﹣2，0），B（0，1）两点，与反比例函数的图象在第一象限交于点C（4，n），求一次函数和反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高3米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有27米的距离（B，F，C在一条直线上）．

    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈，cos22°≈，tan22°≈）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）若m为负整数，求此时方程的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

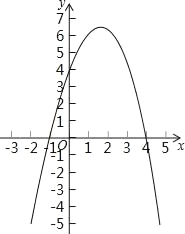
    【题目】已知二次函数y=﹣x2+3x+4的图象如图：（直接写答案）

    （1）方程﹣x2+3x+4=0的解是　 　；

    （2）不等式﹣x2+3x+4＞0的解集是　 　；

    （3）不等式﹣x2+3x+4＜0的解集是　 　．

    查看答案和解析>>

    同步练习册答案