
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,
,![]() .
.
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() 为等边三角形,求
为等边三角形,求![]() 的度数.
的度数.

【答案】(1)证明见解析;(2)∠A=60°.
【解析】
(1)证明△DBE≌△CEF得到DE=EF,即可得到结论;
(2)由已知得到∠DEF=60°,根据外角的性质及△DBE≌△CEF得到∠DEF+∠CEF=∠B+∠BDE,求得∠B =∠DEF=60°,再根据AB=AC即可求出![]() 的度数.
的度数.
(1)证明:∵AB=AC,∴∠B=∠C.
在△DBE 和△CEF 中,
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF 是等腰三角形.
(2)∵△DEF为等边三角形,
∴∠DEF=60°.
∵△DBE≌△CEF,∴∠BDE=∠CEF.
∵∠DEF+∠CEF=∠B+∠BDE,∴∠B =∠DEF=60°.
∴∠C=∠B=60°.
∴∠A=180°-∠B-∠C=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
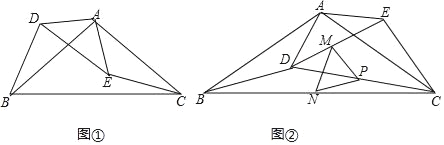
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
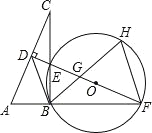
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线相交于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
(1)求证:△HGF∽△HFB;
(2)求证:BD=![]() EF;
EF;
(3)连接HE,若AB=2,求△HEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
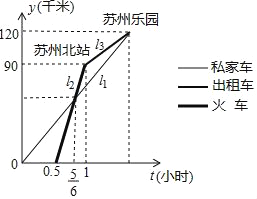
【题目】“五一”期间小明和小丽相约到苏州乐园游玩,小丽乘私家车从上海出发30分钟后,小明乘坐火车从上海出发,先到苏州北站,然后再乘出租车去游乐园(换乘时间忽略不计),两人恰好同时到达苏州乐园,他们离上海的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象信息解决下面问题:
(1)本次火车的平均速度_________千米/小时?
(2)当小明到达苏州北站时,小丽离苏州乐园的距离还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
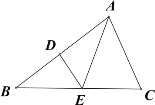
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
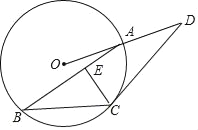
【题目】如图,已知点A,B,C在半径为4的⊙O上,过点C作⊙O的切线交OA的延长线于点D.
(Ⅰ)若∠ABC=29°,求∠D的大小;
(Ⅱ)若∠D=30°,∠BAO=15°,作CE⊥AB于点E,求:
①BE的长;
②四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
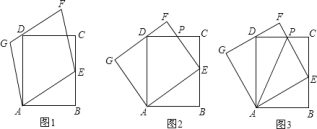
【题目】如图![]() 、图
、图![]() 、图
、图![]() ,在矩形
,在矩形![]() 中,
中,![]() 是
是![]() 边上的一点,以
边上的一点,以![]() 为边作平行四边形
为边作平行四边形![]() ,使点
,使点![]() 在
在![]() 的对边
的对边![]() 上,
上,
![]() 如图
如图![]() ,试说明:平行四边形
,试说明:平行四边形![]() 的面积与矩形
的面积与矩形![]() 的面积相等;
的面积相等;
![]() 如图
如图![]() ,若平行四边形
,若平行四边形![]() 是矩形,
是矩形,![]() 与
与![]() 交于点
交于点![]() ,试说明:
,试说明:![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上;
四点在同一个圆上;
![]() 如图
如图![]() ,若
,若![]() ,平行四边形
,平行四边形![]() 是正方形,且
是正方形,且![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,判断以
,判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com