【题目】某玩具店用2000元购进一批玩具，面市后，供不应求，于是店主又购进同样的玩具，所购的数量是第一批数量的3倍，但每件进价贵了4元，结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元，且两批玩具全部售完．
（1）第一次购进了多少件玩具？
（2）求该玩具店销售这两批玩具共盈利多少元？
全程金卷系列答案
快乐5加2金卷系列答案科目：初中数学 来源： 题型：
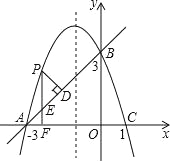
【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过A、B、C三点，已知点A（﹣3，0），B（0，3），C（1，0）．
（1）求此抛物线的解析式．
（2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，抛物线y=
x2+
x﹣
与x轴交于A、B两点（点A在点B的左侧）与y轴交于点C，直线BE⊥BC与点B，与抛物线的另一交点为E．
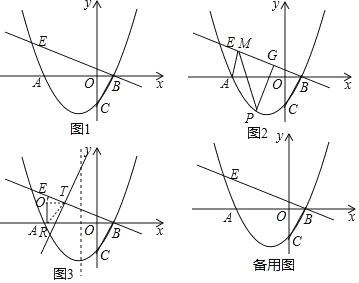
（1）如图1，求点E的坐标；
（2）如图2，若点P为x轴下方抛物线上一动点，过P作PG⊥BE与点G，当PG长度最大时，在直线BE上找一点M，使得△APM的周长最小，并求出周长的最小值．
（3）如图3，将△BOC在射线BE上，设平移后的三角形为△B′O′C′，B′在射线BE上，若直线B′C′分别与x轴、抛物线的对称轴交于点R、T，当△O′RT为等腰三角形时，求R的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A、B两点，与y轴交于点C，对称轴为直线x=﹣1，点B的坐标为（1，0），则下列结论：①AB=4；②b2﹣4ac＞0；③ab＜0；④a2﹣ab+ac＜0，其中正确的结论有（ ）个．
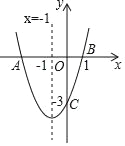
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在平面直角坐标系xOy中，正比例函数y=
x的图象经过点A，点A的纵坐标为4，反比例函数y=
的图象也经过点A，第一象限内的点B在这个反比例函数的图象上，过点B作BC∥x轴，交y轴于点C，且AC=AB．求：
（1）这个反比例函数的解析式；
（2）直线AB的表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
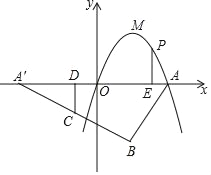
【题目】抛物线y=ax2+bx的顶点M（
，3）关于x轴的对称点为B，点A为抛物线与x轴的一个交点，点A关于原点O的对称点为A′；已知C为A′B的中点，P为抛物线上一动点，作CD⊥x轴，PE⊥x轴，垂足分别为D，E．
（1）求点A的坐标及抛物线的解析式；
（2）当0＜x＜2时，是否存在点P使以点C，D，P，E为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷，在一次购物中，张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付．
(1)张华用“微信”支付的概率是______．
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率．(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
