
【题目】小明家承包了40亩大棚蔬菜,分别种植甲、乙两种蔬菜,有关成本,销售额如下表:
每亩成本 | 每亩销售额 | |
甲 |
| 4 |
乙 | 3 |
|
![]() 年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?
年,小明家种植甲蔬菜30亩,乙蔬菜10亩,求小明家这一年收益多少万元?
![]() 年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩?
年,小明家继续用这40亩全部种植甲乙两种蔬菜,计划投入成本不少于141万元,若每亩种植成本、销售额和2015年一样,要获得最大收益,他家应该种植甲乙两种蔬菜各多少亩?
![]() 已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克
已知甲种蔬菜每亩需要有机肥600千克,乙种蔬菜每亩需要有机肥800千克![]() 根据
根据![]() 中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克?
中的种植亩数,为节约运输成本,实际使用的运输每次装载的总量是计划的每次装载的总量的4倍,结果运输种植所需全部有机肥比原计划减少3次,求小明家原定的运输车辆每次可装载有机肥多少千克?
【答案】(1)17(2) 要获得最大收益,应种植甲蔬菜35亩,种植乙种蔬菜5亩(3)小明家原定的运输车辆每次可装载有机肥6250千克
【解析】试题分析:(1)根据一年的收益等于两种蔬菜的收益之和列式计算即可得解;(2)设种甲种蔬菜x亩,则种乙种蔬菜(40-x)亩,根据总成本列出不等式求出x的取值范围,然后设总收益为W,表示出收益的函数关系式,再根据一次函数的增减性解答;(3)设原定运输车辆每次可装载有机肥mkg,根据实际运输的有机肥比原计划运输的有机肥减少了3次列出方程,求解即可.
试题解析:
![]() 由题意得,
由题意得,![]() 万元
万元![]() ,
,
答:小明家这一年收益17万元;
![]() 设种甲种蔬菜x亩,则种乙种蔬菜
设种甲种蔬菜x亩,则种乙种蔬菜![]() 亩,
亩,
根据题意得,![]() ,
,
解得:![]() ,
,
设总收益为W,则![]() ,
,
![]() ,
,
![]() ,
,
![]() 随x的增大而减小,
随x的增大而减小,
![]() 当
当![]() 时,获得最大收益,
时,获得最大收益,
答:要获得最大收益,应种植甲蔬菜35亩,种植乙种蔬菜5亩;
![]() 设原定运输车辆每次可装有机肥mkg,则实际每次装载4mkg,
设原定运输车辆每次可装有机肥mkg,则实际每次装载4mkg,
需要运输的有机肥料吨数为:![]() ,
,
根据题意得,![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,
是原方程的解,
答:小明家原定的运输车辆每次可装载有机肥6250千克.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
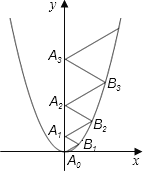
【题目】二次函数![]() 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2008在y轴的正半轴上,点B1,B2,B3,…,B2008在二次函数![]() 位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ![]() ;
;
其中正确的是(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当a=0时,方程ax+b=0(其中x是未知数,b是已知数)的解的情况是( )
A. 唯一解B. 无解C. 有无数多个解D. 无解或有无数多个解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com