
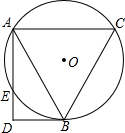
 如图,等边△ABC内接于⊙O,BD切⊙O于B,AD⊥BD于D,AD交⊙O于E,⊙O的半径为1,则AE=1.
如图,等边△ABC内接于⊙O,BD切⊙O于B,AD⊥BD于D,AD交⊙O于E,⊙O的半径为1,则AE=1. 分析 作OH⊥BC,OF⊥AD,连结OB、OC、DE,根据等边三角形的性质得∠BOC=120°,则∠OBC=30°,可计算得OH=$\frac{1}{2}$,BH=$\frac{\sqrt{3}}{2}$,再根据垂径定理得BC=2BH=$\sqrt{3}$;然后根据切线的性质得OB⊥DB,易判断四边形BDFO为矩形,则DF=OB=1,设AF=x,则EF=x,DE=1-x,AD=1+x,接着根据切割线定理得到BD2=1-x2,然后在Rt△ABD中利用根据定理可得到(1+x)2+1-x2=($\sqrt{3}$)2,解得x=$\frac{1}{2}$,由此得到AE=2x=1.
解答 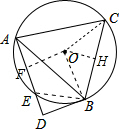 解:如图所示:作OH⊥BC,OF⊥AD,连结OB、OC、DE.
解:如图所示:作OH⊥BC,OF⊥AD,连结OB、OC、DE.
∵△ABC为等边三角形,
∴∠BOC=120°.
∴∠OBC=30°.
在Rt△OBH中,OH=$\frac{1}{2}$OB=$\frac{1}{2}$,
∴BH=$\sqrt{3}$OH=$\frac{\sqrt{3}}{2}$.
∵OH⊥BC,
∴BH=CH.
∴BC=2BH=$\sqrt{3}$,
∴AB=$\sqrt{3}$.
∵BD切⊙O于B,
∴OB⊥DB.
∵AD⊥BD,OH⊥BC,
∴∠OBD=∠D=∠DFO=90°,且AF=EF.
∴四边形BDFO为矩形.
∴DF=OB=1.
设AF=x,则EF=x,DE=1-x,AD=1+x,
∵BD⊙O的切线,
∴BD2=DE•DA=(1-x)(1+x)=1-x2.
在Rt△ABD中,AD2+BD2=AB2,
∴(1+x)2+1-x2=($\sqrt{3}$)2,解得x=$\frac{1}{2}$.
∴AE=2x=1.
故答案为:1.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、勾股定理、切割线定理和等边三角形性质,掌握本题的辅助线的作法是解题的关键.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )| A. | $\frac{2}{3}$m2 | B. | 1m2 | C. | $\frac{3}{2}$m2 | D. | 3m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com