Question

【题目】在△ABC中，CE，BD分别是边AB，AC上的高，F是BC边上的中点．

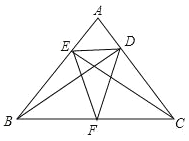
（1）指出图中的一个等腰三角形，并说明理由．

（2）若∠A=x°，求∠EFD的度数（用含x的代数式表达）．

（3）猜想∠ABC和∠EDA的数量关系，并证明．

Answer 1

【答案】（1）△DEF是等腰三角形；

（2）∠EFD=180°﹣2x°；

（3）ABC=∠EDA．

【解析】

试题分析：（1）根据直角三角形的性质得到EF=BC，DF=BC，等量代换即可；

（2）根据三角形内角和定理和等腰三角形的性质计算；

（3）根据圆内接四边形的性质解答．

试题解析：（1）△DEF是等腰三角形．

∵CE，BD分别是边AB，AC上的高，F是BC边上的中点，

∴EF=BC，DF=BC，

∴EF=DF，

∴△DEF是等腰三角形；

（2）∵FE=FB，FD=FC，

∴∠FEB=∠FBE，∠FDC=∠FCD，

∴∠FEB+∠FDC=∠FBE+∠FCD=180°﹣∠A=180°﹣x°，

∠AED+∠ADE=180°﹣∠A=180°﹣x°，

∴∠FED+∠FDE=360°﹣（180°﹣x°）﹣（180°﹣x°）=2x°，

∴∠EFD=180°﹣2x°；

（3）∠ABC=∠EDA．

∵∠BEC=∠BDC=90°，

∴B、E、D、C四点共圆，

∴∠ABC=∠EDA．