

分析 (1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)先设出点M坐标,得出三角形MOA面积,进而确定出点M的坐标.
(3)根据平移规律,可得新抛物线,根据联立抛物线与OP,可得C、D点的横坐标,根据勾股定理,可得答案.
解答 解:(1)依题意-52+5m+m-4=-5,
∴m=4,
∴y=-x2+4x=-(x-2)2+4
∴顶点P(2,4);
(2)如图1,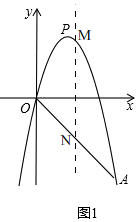
∵A(5,-5),
∴OA的解析式为y=-x,
设M(m,-m2+4m),(0<m<5)
∴N(m,-m),
∴MN=-m2+4m+m=-m2+5m,
∴S△MOA=$\frac{1}{2}$MN•|xA-xO|=$\frac{1}{2}$•(-m2+5m)•5=-$\frac{5}{2}$(m2-5m)=-$\frac{5}{2}$(m-$\frac{5}{2}$)2+$\frac{125}{8}$
∴当m=$\frac{5}{2}$时,△MOA的面积取得最大,此时的点M坐标($\frac{5}{2}$,$\frac{15}{4}$).
(3)在抛物线平移的过程中,线段CD的长度是为定值,
∵直线OP的解析式为y=2x,
∴可设新抛物线解析式为y=-(x-a)2+2a
联立抛物线与OP,
$\left\{\begin{array}{l}{y=-(x-a)^{2}+2a}\\{y=2x}\end{array}\right.$,
∴-(x-a)2-$\frac{3}{2}$a=-$\frac{3}{2}$x,
∴x1=a,x2=a-2,x1-x2=2;
y1=2x1=2a,y2=2x2=2(a-2),y1-y2=4;
∴CD的长度=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{4+16}$=2$\sqrt{5}$
∴在抛物线平移的过程中,线段CD的长度是定值,定值为2$\sqrt{5}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,确定出三角形MOA的面积是解题关键,又利用了解方程组得出P点坐标;利用勾股定理得出CD的.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
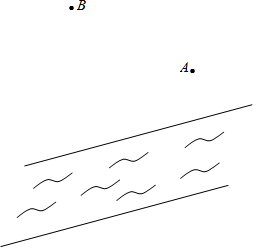 如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.
如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com