
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
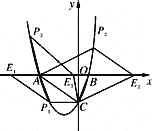
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式![]()
(2)四边形ABCD面积有最大值为![]() ;
;
(3)存在3个点符合题意,坐标分别是P1(-2,-3), ![]() ,
, ![]()
【解析】试题分析:(1)、根据题意得出点B和点C的坐标,然后代入函数解析式求出答案;(2)、首先根据点A和点C的坐标得出直线AC的解析式,然后过点D作DM∥y轴分别交线段AC和x轴于点M,N,设点M的坐标为(m,-m-3),从而得出点D的坐标,求出DM的长度,根据二次函数的性质求出DM的最大值,得出面积的最大值;(3)、①、过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,,将C(0,-3)代入函数解析式求出点P的坐标;②、平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,设出点P的坐标为(x,3),然后代入函数解析式求出点P的坐标.
试题解析:(1)、∵OC=3OB,B(1,0),∴C(0,-3). 把点B,C的坐标代入![]() ,得
,得![]()
∴抛物线的解析式![]()
(2)、由A(-3,0),C(0,-3)得直线AC的解析式为![]() ,
,
如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
设M![]() 则D
则D![]() ,
, ![]()
∴-1<0,∴当x=![]() 时,DM有最大值
时,DM有最大值![]() ∴S四边形ABCD=S△ABC+S△ACD
∴S四边形ABCD=S△ABC+S△ACD![]()
此时四边形ABCD面积有最大值为![]() .
.
(3)、存在
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,
此时四边形ACP1E1为平行四边形. ∵C(0,-3),令![]()
∴![]() ,
, ![]() .∴P1(-2,-3).
.∴P1(-2,-3).
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,∵C(0,-3),
∴可令P(x,3), ![]() ,得
,得![]() 解得
解得![]() ,
, ![]()
此时存在点![]() ,
,![]()
综上所述,存在3个点符合题意,坐标分别是P1(-2,-3), ![]()
![]()



科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD,点 E,F 分别在 AD,CD 上,且DE=CF,AF 与 BE 相交于点G.
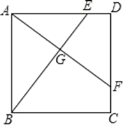
(1)求证:AF⊥BE;
(2)若 AB=6,DE=2,AG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=3x的图象与反比例函数y=![]() 的图象交于点A(1,m)和点B.
的图象交于点A(1,m)和点B.
(1)求m的值和反比例函数的解析式.
(2)观察图象,直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )

A. 60° B. 90° C. 30° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是∠AOB的平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.下列结论 不一定成立的是( )

A.∠AOP=∠BOPB.PC=PD
C.∠OPC=∠OPDD.OP=PC+PD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com