
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点
在第四象限的抛物线上,求点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,问在
,问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

【答案】![]()
![]() ;
;![]() 点
点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ;
;![]() 存在.
存在.![]() ,或
,或![]() .
.
【解析】
(1)将A(-1,0)、C(0,-3)两点坐标代入抛物线y=ax2+bx-3a中,列方程组求a、b的值即可;
(2)将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;
(3)分两种情形①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,②连接BD′,过点C作CP′∥BD′,交x轴于P′,
分别求出直线CP和直线CP′的解析式即可解决问题.
![]() 将
将![]() 、
、![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() ,
,
解得![]() ,
,
∴![]() ;
;
![]() 将点
将点![]() 代入
代入![]() 中,得
中,得
![]() ,
,
解得![]() 或
或![]() ,
,
∵点![]() 在第四象限,
在第四象限,
∴![]() ,
,
∵直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ;
;
![]() 存在.
存在.
过![]() 点作
点作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于
于![]() 点(如图),
点(如图),
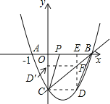
∵![]() ,
,
∴![]() ,
,
又∵![]() 轴,四边形
轴,四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
设![]() 与
与![]() 相交于
相交于![]() 点
点![]() ,
,
易求![]() 解析式为:
解析式为:![]() ,
,
由![]() ,得到关于
,得到关于![]() 的方程,解方程后,得
的方程,解方程后,得![]() ;
;
于是,![]() 点坐标为:
点坐标为:![]() ;
;
于是![]() 解析式为:
解析式为:![]() ,
,
令![]() 方程中,
方程中,![]() ,则
,则![]() ,
,
所以,![]() 点坐标为:
点坐标为:![]() ,
,
∴![]() ,或
,或![]() .
.


科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,如图所示l1和l2分别表示每辆车的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系.

(1)哪条线表示每辆车改装后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系?
(2)每辆车的改装费b= 元,正常营运 天后,就可以从节省的燃料费中收回改装成本;
(3)每辆车改装前每天的燃料费为 元;改装后每天的燃料费为 元;
(4)直接写出每辆车改装前、后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是BC边上的高,点E是AC边的中点,点P是AD上的一个动点,当PC+PE最小时,∠CPE的度数是( )

A.30°B.45°C.60°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩.
(1)小明和小刚都在本周日上午去游玩的概率为 ;
(2)求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com