
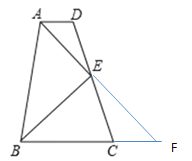
【题目】已知,如图,AD∥BC,AE平分∠BAD,点E是CD的中点.
(1)求证:AB=AD+BC
(2)求证:AE⊥BE

【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1) 延长AE交BC的延长线于点F,根据角平分线和平行线的性质得到![]() ,然后等角对等边AB=BF ,再证明△FCE≌△ADE,进而等量代换求解;(2)由全等得出AE=EF,然后利用等腰三角形三线合一的性质,即可得结论;
,然后等角对等边AB=BF ,再证明△FCE≌△ADE,进而等量代换求解;(2)由全等得出AE=EF,然后利用等腰三角形三线合一的性质,即可得结论;
解:如图:延长AE交BC的延长线于点F,
∵AE平分∠BAD
∴![]()
∵E是DC中点
∴DE=CE
∵AD∥BC
∴![]()
∴![]()
∴AB=BF
又∵在△FCE和△ADE中,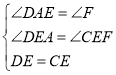
∴△FCE≌△ADE,
∴AD=CF
∴AB=BF=BC+CF=BC+AD
即AB=AD+BC
(2)由(1)可知△FCE≌△ADE
∴AE=FE
又∵BA=BF
∴根据等腰三角形三线合一的性质可知AE⊥BE.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
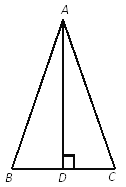
【题目】如图,△ABC中,AD⊥BC,垂足是D.小莉说:当AB+BD=AC+CD时,则△ABC是等腰三角形.她的说法正确吗,如正确,请证明;如不正确,请举反例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
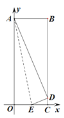
【题目】如图,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐 标系.已知AO=13,AB=5,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.则点E的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若在一个两位正整数N的个位数字与十位数字之间添上数字6,组成一个新的三位数,我们称这个三位数为N的“至善数”,如34的“至善数为364”;若将一个两位正整数M加6后得到一个新数,我们称这个新数为M的“明德数”,如34的“明德数为40”.
(1)30的“至善数”是 ,“明德数”是 .
(2)求证:对任意一个两位正整数A,其“至善数”与“明德数”之差能被9整除;
(3)若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半,求B的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
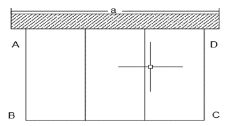
【题目】如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长![]() 米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
(1)若墙长![]() 米,求AB、BC的长.
米,求AB、BC的长.
(2)若![]() 米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点
在第四象限的抛物线上,求点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,问在
,问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有![]() 个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为
个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为![]() .
.
![]() 求口袋中白球的个数;
求口袋中白球的个数;
![]() 如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com