
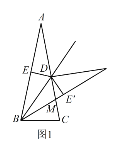
����Ŀ����1����ͼ1������������ֽƬ��AB=AC,��BAC=30������ͼ2��ֽƬ��DE�۵���ʹ�õ�A���B�غϣ���ʱ��DBC= ��

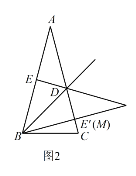
��2���ڣ�1���������£�����DEB��ֱ��BD�۵�����Eǡ�������߶�DC�ϵĵ�E��������ͼ3����ʱ��E��BC= ��

��3������ȡһ�ŵ���������ֽƬABC![]() ��AB=AC����ֱ��DE�۵�����D
��AB=AC����ֱ��DE�۵�����D![]() ,E�ֱ�Ϊ�ۺ���ֱ��AC
,E�ֱ�Ϊ�ۺ���ֱ��AC![]() ��
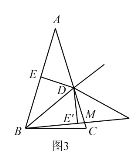
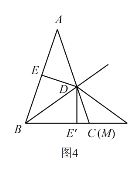
��![]() AB�Ľ��㣩��ʹ�õ�A���B�غϣ��ٽ�����ͼ����ֱ��BD�۵���ʹ��E���ڵ�E����λ�ã�ֱ��BE����ֱ��AC���ڵ�M�����BAC=m����m��90���������۵����ͼ�Σ���ֱ��д����Ӧ�ġ�MBC�Ĵ�С�����ú�m�Ĵ���ʽ��ʾ��
AB�Ľ��㣩��ʹ�õ�A���B�غϣ��ٽ�����ͼ����ֱ��BD�۵���ʹ��E���ڵ�E����λ�ã�ֱ��BE����ֱ��AC���ڵ�M�����BAC=m����m��90���������۵����ͼ�Σ���ֱ��д����Ӧ�ġ�MBC�Ĵ�С�����ú�m�Ĵ���ʽ��ʾ��
���𰸡���1��![]() ��2��
��2��![]() ��3���𰸲�Ψһ�����������
��3���𰸲�Ψһ�����������
��������
��1�����ݡ�DBC=��ABC-��DBE���㼴�ɣ�
��2�����ݡ�E��BC=��DBC-��DBE�����㼴�ɣ�
��3�����ݸ�ͼ�������ۼ��ɣ�![]() ʱ��
ʱ��![]() ��
��![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�![]() ʱ��
ʱ��![]() ��
��![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�![]() ʱ��
ʱ��![]() ��
��![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�![]() �������ڵ�
�������ڵ�![]() ��
��![]() ʱ��
ʱ��![]() .
.
��1���ߡ�ABC=30����AB=AC,
���ABC=��ACB=75����
����ADE�۵�����BDE�����DBE=��A=30����
���DBC=��ABC-��DBE=45��.
���Դ�Ϊ45��.
��2������DBE�۵�����DBE��,
���DB E��=��DBE=30����
���E��BC=��DBC-��DBE��=15��.
���Դ�Ϊ15��.
��3����ͼ![]() ��
��
![]() ʱ��
ʱ��![]() ��
��
��ͼ![]() ��
��
![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�
��ͼ![]() ��
��
![]() ʱ��
ʱ��![]() ��
��
��ͼ![]() ��
��
![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�
��ͼ![]() ��
��
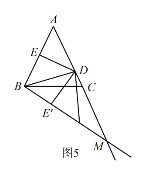
![]() ʱ��
ʱ��![]() ��
��
��ͼ![]() ��
��
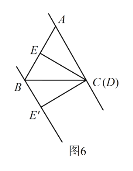
![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�![]() �������ڵ�
�������ڵ�![]() ��
��
��ͼ![]() ��
��
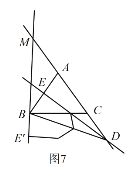
![]() ʱ��
ʱ��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DB��AC����DB=![]() AC��E��AC���е㣮
AC��E��AC���е㣮
��1����֤��BC=DE��
��2������AD��BE������BAC=��C����֤���ı���DBEA�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A�������Ϊ��a��6����AB��x���ڵ�B��cos��OAB�T![]() ������������y=
������������y=![]() ��ͼ���һ֧�ֱ�AO��AB�ڵ�C��D���ӳ�AO��������������ͼ�����һ֧�ڵ�E����֪��D��������Ϊ
��ͼ���һ֧�ֱ�AO��AB�ڵ�C��D���ӳ�AO��������������ͼ�����һ֧�ڵ�E����֪��D��������Ϊ![]() ��
��
��1�����������Ľ���ʽ��
��2����ֱ��EB�Ľ���ʽ��
��3����S��OEB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ1�ĵȱߡ�ABC�ı�AB��һ��P��PE��AC�ڵ�E��QΪBC�ӳ�����һ�㣬��PA=CQʱ������PQ��AC�ڵ�D����DE�ij�Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�У���BAC=90����AB=AC=AD��AD��BC�ڵ�P����CAD=30����AC=6����
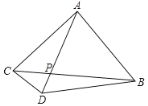
��1����BDC�Ķ�����
��2����ABD���ܳ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽�������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȣ���SSA�����Ƿ����ж�����������ȫ��ʱ��������Ʋ�ͬ���ν���̽����
��1�����磬����B �����ʱ����ͼ ��BC=EF����B=��E�������� EM ���е� D��ʹ DF=AC���ó߹滭�����������ĵ� D�����ABC �͡�DEF �Ĺ�ϵ��( )��
A.ȫ�� B. ��ȫ�� C. ��һ��ȫ��

���ǽ�һ�����������ȷ�������������ε���״����ô��SSA���dz�����.
��2�����磬��֪����ͼ������ǡ�ABC ����ǡ�DEF �У�AC=DF��BC=EF����B=��E. ��֤����ABC�ա�DEF.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A������ B��ƹ����C����ë�� D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺


��1����α������ѧ�������� ���ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB=17cm��AC=10cm��![]() ���ϵĸ�AD=8cm�����
���ϵĸ�AD=8cm�����![]() �ij�Ϊ�� ��
�ij��� ��
A.![]() B.
B.![]() ��
��![]() C.
C.![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com