Question

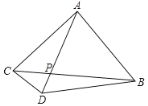
【题目】如图△ABC中，∠BAC=90°，AB=AC=AD，AD交BC于点P，∠CAD=30°，AC=6，求：

（1）∠BDC的度数，

（2）△ABD的周长

Answer 1

【答案】（1）1350（2）18

【解析】

（1）根据∠BAC=90°，∠CAD=30°可先求出∠DAB=60°，因为AB=AD，从而得出∠ADB的度数，之后利用AD=AC得出∠ADC度数，二者相加即可得出答案；

（2）由（1）可得△ABD是等边三角形，进而得出答案即可..

（1）∵∠BAC=90°，∠CAD=30°，

∴∠DAB=60°，

∵AD=AB,

∴△ABD是等边三角形，

∴∠ADB=60°，

又∵∠CAD=30°，AC=AD,

∴∠ADC=75°，

∴∠BDC=∠ADB+∠ADC=135°

（2）由（1）得△ABD是等边三角形，

∵AC=6，

∴AB=AD=BD=AC=6,

∴△ABD的周长为18.