【题目】如图，AB为⊙O的直径，C、D是⊙O上的点，且OC∥BD，AD分别与BC、OC相交于 点E、F．若∠CBD=36°，则下列结论中不正确的是
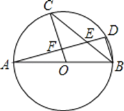
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，过边长为3的等边三角形ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，问：若PA＝CQ时，连接PQ交AC边于D，求DE的长？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，在△ABC中，BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线．
①若∠A＝70°，求∠BDC的度数．
②∠A＝α，请用含有α的代数式表示∠BDC的度数．(直接写出答案)
（2）如图2，BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线．若∠A＝α，请用含有α的代数式表示∠BEC的度数．
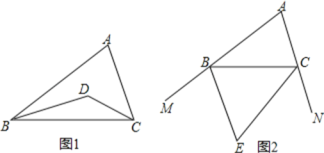
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】陈老师为了解七班
同学对新闻、体育、娱乐、动画四类电视节目的喜欢情况，调查了全班
名同学(每名同学必选且只能选择这四类节目中的一类)，并将调查结果绘制成如下不完整的条形统计图和扇形统计图．根据两图提供的信息，解答下列问题:
求喜欢娱乐节目的人数，并将条形统计图补充完整；
求扇形统计图中喜欢体育节目的人数占全班人数的百分比和圆心角
的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图有一张简易的活动小餐桌，现测得OA=OB=30cm，OC=OD=50cm，桌面离地面的高度为40cm，则两条桌腿的张角∠COD的度数为______度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零.由此可得：如果mx+n=0，其中m、n为有理数，x为无理数，那么m=0且n=0.
（1）如果
，其中a、b为有理数，那么a= ，b= .
（2）如果
，其中a、b为有理数，求a+2b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读与理解：
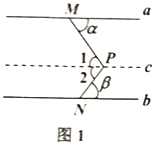
如图1，直线
，点P在a，b之间，M，N分别为a，b上的点，P，M，N三点不在同一直线上，PM与a的央角为
，PN与b的夹角为
，则
．
理由如下：
过P点作直线
，因为，所以
（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．所以
，
．（两直线平行，内错角相等），所以
，即．
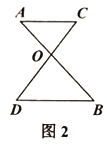
计算与说明：
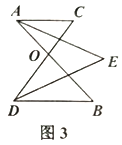
已知：如图2，AB与CD交于点O．
（1）.若
，求证：
；
（2）2.如图3，已知
，AE平分
，DE平分
．
①若
，
，请你求出
的度数；
②请问：图3中，
与有怎样的数量关系？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
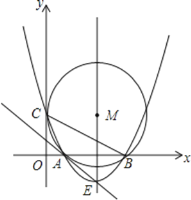
【题目】如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A，B两点．
（1）请直接写出A，B，C三点的坐标，并求出过这三点的抛物线解析式；
（2）设（1）中抛物线解析式的顶点为E，
求证：直线EA与⊙M相切；
（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形？
如果存在，请求出点P的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 AB∥CD，点 M、N 分别是 AB、CD 上两点，点 G 在 AB、CD 之间，连接 MG、NG．
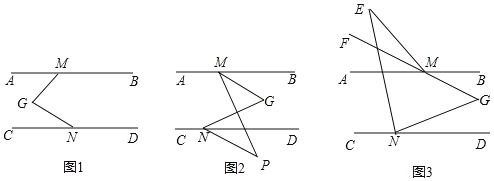
（1）如图 1，若 GM⊥GN，求∠AMG+∠CNG 的度数；
（2）如图 2，若点 P 是 CD 下方一点，MG 平分∠BMP，ND 平分∠GNP，已知∠BMG＝40°，求∠MGN+∠MPN的度数；
（3）如图 3，若点 E 是 AB 上方一点，连接 EM、EN，且 GM 的延长线 MF 平分∠AME，NE 平分∠CNG，2∠MEN+∠MGN＝102°，求∠AME 的度数．（直接写出结果）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
