
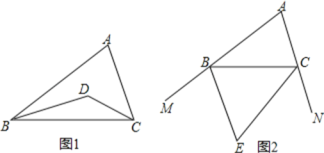
【题目】(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
①若∠A=70°,求∠BDC的度数.
②∠A=α,请用含有α的代数式表示∠BDC的度数.(直接写出答案)
(2)如图2,BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线.若∠A=α,请用含有α的代数式表示∠BEC的度数.
【答案】(1)①125°;②∠A=90°+![]() α;(2)∠BEC=90°﹣
α;(2)∠BEC=90°﹣![]() α.
α.
【解析】
(1)①根据角平分线定义可得到∠ABD=∠CBD,∠BCD=∠ACD,再根据三角形内角和定理得到∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,利用等量代换可得2(180°﹣∠BDC)+∠A=180°,进而得到∠BDC=90°+![]() ∠A;②直接利用①的结论写出即可
∠A;②直接利用①的结论写出即可
(2)利用角平分线定义得到∠EBC=![]() ∠MBC,∠BCE=
∠MBC,∠BCE=![]() ∠BCM,再由三角形外角性质得到∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A,进而得∠EBC+∠BCE=
∠BCM,再由三角形外角性质得到∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A,进而得∠EBC+∠BCE=![]() (∠MBC+∠BCN)=
(∠MBC+∠BCN)=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A,再在△DBC中利用内角和定理得到∠BEC=180°﹣(∠EBC+∠BCE),进行化简即可得到结论.
∠A,再在△DBC中利用内角和定理得到∠BEC=180°﹣(∠EBC+∠BCE),进行化简即可得到结论.
解:(1)①∵∠ABC,∠ACB的平分线相交于点D,
∴∠ABD=∠CBD,∠BCD=∠ACD,
∵∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,
∴2∠DBC+2∠BCD+∠A=180°,
∴2(180°﹣∠BDC)+∠A=180°,
∴∠BDC=90°+![]() ∠A,
∠A,
∵∠A=70°,
∴∠BDC=90°+![]() ×70°=90°+35°=125°.
×70°=90°+35°=125°.
②利用①得到的∠BDC=90°+![]() ∠A,直接表示出∠BDC=90°+
∠A,直接表示出∠BDC=90°+![]() α.
α.
(2)∵BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线,
∴∠EBC=![]() ∠MBC,∠BCE=
∠MBC,∠BCE=![]() ∠BCM,
∠BCM,
∵∠CBM、∠BCN是△ABC的两个外角
∴∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A
∴∠EBC+∠BCE=![]() (∠MBC+∠BCN)=
(∠MBC+∠BCN)=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A,
∠A,
在△DBC中,
∵∠BEC=180°﹣(∠EBC+∠BCE)
=180°﹣(90°+![]() ∠A)
∠A)
=90°﹣![]() ∠A,且∠A=α,
∠A,且∠A=α,
∴∠BEC=90°﹣![]() α.
α.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,那么下列结论,①
,那么下列结论,①![]() 是等腰三角形;②
是等腰三角形;②![]() ;③若
;③若![]() ,
, ![]() ; ④
; ④![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
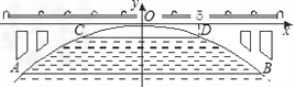
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1+3=22
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52
……
(1)按照此规律,写出第5个等式;
(2)按照此规律,写出第![]() (
(![]() 为正整数)个等式;
为正整数)个等式;
(3)利用(2)中写出的等式,求101+103+105+……+295+297+299的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠B=∠C,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
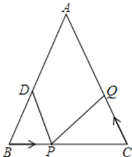
(1)用含t的式子表示PC的长为 ;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据某市2014年至2018年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中判断错误的是( )
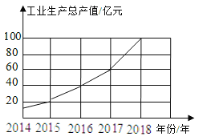
A.2014年至2018年工业生产总值逐年增加
B.2018年的工业生产总值比前一年增加了![]() 亿元
亿元
C.2016年与2017年每一年与前一年比,其增长额相同
D.2015年至2018年,每一年与前一年比,2018年的增长率最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于 点E、F.若∠CBD=36°,则下列结论中不正确的是
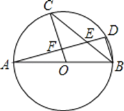
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com