
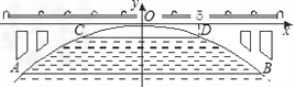
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?
【答案】(1)抛物线的解析式为y=﹣![]() x2;
x2;
(2)要使货车安全通过此桥,货车的速度应超过60千米/时.
【解析】试题分析:根据抛物线在坐标系的位置,设抛物线的解析式为y=ax2,设D、B的坐标求解析式;
试题解析:(1)设抛物线的解析式为y=ax2(a不等于0),桥拱最高点O到水面CD的距离为h米.
则D(5,﹣h),B(10,﹣h﹣3)
∴![]()
解得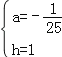
∴抛物线的解析式为y=﹣![]() x2
x2
(2)水位由CD处涨到点O的时间为:1÷0.25=4(小时)
货车按原来速度行驶的路程为:40×1+40×4=200<280
∴货车按原来速度行驶不能安全通过此桥.
设货车速度提高到x千米/时
当4x+40×1=280时,x=60
∴要使货车安全通过此桥,货车的速度应超过60千米/时.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠BCA=90°,AC=BC,点M、N在斜边AB上,且∠MCN=45°,试探究线段AM,,MN,BN之间的关系,并说明理由。.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,问:若PA=CQ时,连接PQ交AC边于D,求DE的长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-1,0),B(2,-3)两点在一次函数y2=-x+m与二次函数y1=ax2+bx-3的图象上.
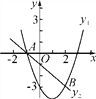
(1)求m的值和二次函数的解析式;
(2)请直接写出使y2>y1时,自变量x的取值范围;
(3)说出所求的抛物线y1=ax2+bx-3可由抛物线y=x2如何平移得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x-h)2+k的形式;
(2)用五点法画出此函数图象的示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:
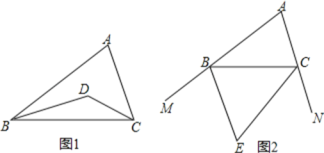
【题目】(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
①若∠A=70°,求∠BDC的度数.
②∠A=α,请用含有α的代数式表示∠BDC的度数.(直接写出答案)
(2)如图2,BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线.若∠A=α,请用含有α的代数式表示∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师为了解七班![]() 同学对新闻、体育、娱乐、动画四类电视节目的喜欢情况,调查了全班
同学对新闻、体育、娱乐、动画四类电视节目的喜欢情况,调查了全班![]() 名同学(每名同学必选且只能选择这四类节目中的一类),并将调查结果绘制成如下不完整的条形统计图和扇形统计图.根据两图提供的信息,解答下列问题:
名同学(每名同学必选且只能选择这四类节目中的一类),并将调查结果绘制成如下不完整的条形统计图和扇形统计图.根据两图提供的信息,解答下列问题:

![]() 求喜欢娱乐节目的人数,并将条形统计图补充完整;
求喜欢娱乐节目的人数,并将条形统计图补充完整;
![]() 求扇形统计图中喜欢体育节目的人数占全班人数的百分比和圆心角
求扇形统计图中喜欢体育节目的人数占全班人数的百分比和圆心角![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
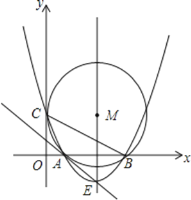
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
(1)请直接写出A,B,C三点的坐标,并求出过这三点的抛物线解析式;
(2)设(1)中抛物线解析式的顶点为E,
求证:直线EA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形?
如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com