【题目】如图正比例函数y=2x的图像与一次函数 
的图像交于点A（m,2）,一次函数的图象经过点B（-2，-1）与y轴交点为C与x轴交点为D.
（1）求一次函数的解析式；
（2）求
的面积。
【答案】（1）一次函数的解析式为
；（2）1.
【解析】（1）首先根据正比例函数解析式求得m的值，再进一步运用待定系数法求得一次函数的解析式；
（2）根据（1）中的解析式，令y=0求得点C的坐标，从而求得三角形的面积.
解：（1）由题可得，把点A（m,2）代入正比例函数y=2x 得
2＝2m
m=1
所以点A（1,2）
因为一次函数图象又经过点B（-2,-1），所以
解方程组得
这个一次函数的解析式为
（2）因为一次函数图象与x轴的交点为D，
所以点D的坐标为（-1,0）
因为
的底为OD=1,高为A点的纵坐标2
所以
“点睛”此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法，关键是根据正比例函数解析式求得m的值.
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
【题目】已知∠AOB＝20°，∠AOC＝4∠AOB，OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是_____________________度
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．
（1）判断BF与AC的数量关系并说明理由；
（2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．
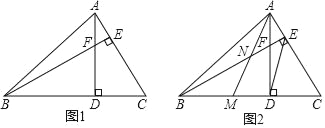
【答案】（1）BF=AC，理由见解析；（2）NE=
AC，理由见解析.
【解析】试题分析：（1）如图1，证明△ADC≌△BDF（AAS），可得BF=AC；
（2）如图2，由折叠得：MD=DC，先根据三角形中位线的推论可得：AE=EC，由线段垂直平分线的性质得：AB=BC，则∠ABE=∠CBE，结合（1）得：△BDF≌△ADM，则∠DBF=∠MAD，最后证明∠ANE=∠NAE=45°，得AE=EN，所以EN=
AC．
试题解析：
（1）BF=AC，理由是：
如图1，∵AD⊥BC，BE⊥AC，
∴∠ADB=∠AEF=90°，
∵∠ABC=45°，
∴△ABD是等腰直角三角形，
∴AD=BD，
∵∠AFE=∠BFD，
∴∠DAC=∠EBC，
在△ADC和△BDF中，
∵
，
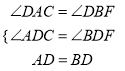∴△ADC≌△BDF（AAS），
∴BF=AC；
（2）NE=
AC，理由是：
如图2，由折叠得：MD=DC，
∵DE∥AM，
∴AE=EC，
∵BE⊥AC，
∴AB=BC，
∴∠ABE=∠CBE，
由（1）得：△ADC≌△BDF，
∵△ADC≌△ADM，
∴△BDF≌△ADM，
∴∠DBF=∠MAD，
∵∠DBA=∠BAD=45°，
∴∠DBA﹣∠DBF=∠BAD﹣∠MAD，
即∠ABE=∠BAN，
∵∠ANE=∠ABE+∠BAN=2∠ABE，
∠NAE=2∠NAD=2∠CBE，
∴∠ANE=∠NAE=45°，
∴AE=EN，
∴EN=
AC．
【题型】解答题
【结束】
17
【题目】已知x1，x2是方程2x2﹣2nx+
n（n+4）=0的两根，且（x1﹣1）（x2﹣1）﹣1=
，求n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某区为争创全国文明卫生城，2016年区政府对区绿化工程投入的资金是2000万元，2018年投的资金是2420万元，且2017年和2018年，每年投入资金的年平均增长率相同．
（1）求该区对区绿化工程投入资金的年平均增长率；
（2）若投入资金的年平均增长率不变，那么该区在2020年需投入资金多少万元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在一个边长为a的正方形木板上锯掉一个边长为b的正方形, 并把余下的部分沿虚线剪开拼成图2的形状.
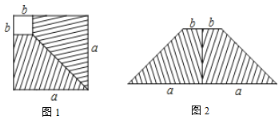
(1)请用两种方法表示阴影部分的面积
图1得： ； 图2得 ；
(2)由图1与图2 面积关系，可以得到一个等式： ；
(3)利用（2）中的等式，已知
，且a+b=8，则a-b= .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知数轴上，一动点Q从原点O出发，沿数轴以每秒2个单位长度的速度来回移动，其移动的方式是：先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…，
（1）动点Q运动3秒时，求此时Q在数轴上表示的数?
（2）当动点Q第一次运动到数轴上对应的数为10时，求Q运动的时间t；
（3）若5秒时，动点Q激活所在位置P点，P点立即以0.1个单位长度/秒的速度沿数轴运动，试求点P激活后第一次与继续运动的点Q相遇时所在的位置.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac>0；②abc<0；③m>2.其中，正确结论的个数是
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：在直角坐标系中，A（﹣2，4）B（﹣4，2）；A1、B1是A、B关于y轴的对称点；
（1）请在图中画出A、B关于原点O的对称点A2，B2（保留痕迹，不写作法）；并直接写出A1、A2、B1、B2的坐标．
（2）试问：在x轴上是否存在一点C，使△A1B1C的周长最小，若存在求C点的坐标，若不存在说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
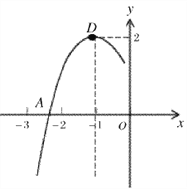
【题目】拋物线
的顶点为D(-1，2)，与x轴的一个交点A在点(-3，0)和(-2，0)之间，其部分图象如图，则以下结论：①
；②当x＞-l时，y随x增大而减小；③a+b+c＜0；④若方程
没有实数根，则m＞2. 其中正确的结论有________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com