
【题目】如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.若以点B为圆心,1.6为半径作圆⊙B,使点M和点N都在⊙B外,则x的取值范围是( )
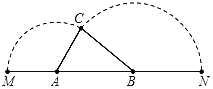
A.1<x<2B.0.6<x<1.6C.1<x<1.6D.1<x<1.4
【答案】D
【解析】
根据旋转的性质得AC=AM=1,BC=BN=3﹣x,根据三角形三边的关系可得到x的取值范围为1<x<2,根据点与圆是位置关系得到不等式进一步确定x的取值范围即可解答问题.
解:∵MN=4,MA=1,AB=x,
∴MB =1+ x,BN=4﹣1﹣x=3﹣x,
∵以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,
∴AC=AM=1,BC=BN=3﹣x,
在△ABC 中,![]() ,
,
∴解得1<x<2,
∵以点B为圆心,1.6为半径作圆⊙B,使点M和点N都在⊙B外,
∴1+x>1.6且3﹣x>1.6,
∴0.6<x<1.4,
∴x的取值范围是1<x<1.4,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB.CD相交于点O,B.D两点立于地面,经测量:
AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,
tan61.9°≈0.553;可使用科学记算器)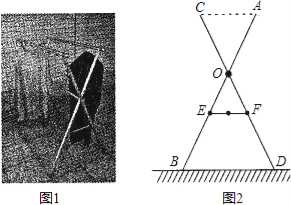
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:矩形旋转中的数学
已知在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为旋转中心,逆时针旋转矩形
为旋转中心,逆时针旋转矩形![]() ,旋转角为
,旋转角为![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 、点
、点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() 、点
、点![]() .
.
操作猜想:
(1)如图①,当点![]() 落在
落在![]() 边上时,求线段
边上时,求线段![]() 的长度;
的长度;
深入探究:
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长度;
的长度;
(3)请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
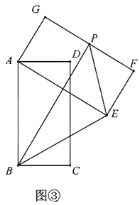
![]() 题:如图③,设点
题:如图③,设点![]() 为边
为边![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,在矩形
,在矩形![]() 旋转过程中,
旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
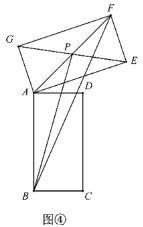
![]() 题:如图④,设点
题:如图④,设点![]() 为矩形
为矩形![]() 对角线交点,连接
对角线交点,连接![]() ,
,![]() ,在矩形
,在矩形![]() 旋转过程中,
旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市红十字预计在2019年儿童节前为郊区某小学发放学习用品,联系某工厂加工学习用品.机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件,若加工1800件这样的产品,机器加工所用的时间是手工加工所用时间的![]() 倍.
倍.
(1)求手工每小时加工产品的数量;
(2)经过调查该小学的小学生的总数不超过1332名,每名小学生分发两个学习用品,工厂领导打算在两天内(48小时)完成任务,打算以机器加工为主,同时人工也参与加工(人工与机器加工不能同时进行),为了保证按时完成加工任务,人工至少要加工多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,为了选拔“阳光大课堂”领操员校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
若任意选择一名领操员的可能性相同
(1)任意选取一名领操员,选到成绩最低领操员的概率是_________.
(2)已知获得10分的选手中,七、八、九年级分别有1人,2人,1人,学校准备从中随机选取两人领操,求恰好选到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
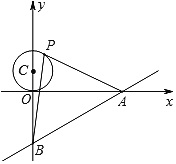
【题目】如图,已知直线y=![]() x﹣6与x轴、y轴分别交于A、B两点,点P是以C(0,3)为圆心,3为半径的圆上一动点,连结PA、PB.
x﹣6与x轴、y轴分别交于A、B两点,点P是以C(0,3)为圆心,3为半径的圆上一动点,连结PA、PB.
(1)求圆心C到直线AB的距离;
(2)求△PAB面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解班级学生数学课前预习的具体情况,郑老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(2)扇形统计图中“课前预习不达标”对应的圆心角度数是 ;
(3)为了共同进步,郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 为图形
为图形![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 直线
直线![]() 垂足为
垂足为![]() ,记
,记![]() 的长度为
的长度为![]() .
.
定义一:若![]() 存在最大值,则称其为“图形
存在最大值,则称其为“图形![]() 到直线
到直线![]() 的限距离”,记作
的限距离”,记作![]() ;
;
定义二:若![]() 存在最小值,则称其为“图形
存在最小值,则称其为“图形![]() 到直线
到直线![]() 的基距离”,记作
的基距离”,记作![]() ;
;
(1)已知直线![]() ,平面内反比例函数
,平面内反比例函数![]() 在第一象限内的图象记作
在第一象限内的图象记作![]() 则
则![]() .
.
(2)已知直线![]() ,点
,点![]() ,点
,点![]() 是
是![]() 轴上一个动点,
轴上一个动点,![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() 求此时
求此时![]() 的取值范围,
的取值范围,
(3)已知直线![]() 恒过定点
恒过定点![]() ,点
,点![]() 恒在直线
恒在直线![]() 上,点
上,点![]() 是平面上一动点,记以点
是平面上一动点,记以点![]() 为顶点,原点为对角线交点的正方形为图形
为顶点,原点为对角线交点的正方形为图形![]()
![]() ,若请直接写出
,若请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
(1)通过配方将它写成![]() 的形式.
的形式.
(2)当![]() 时,函数有最 值,是 .
时,函数有最 值,是 .
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;)当
的增大而增大;)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
(4)该函数图象由![]() 的图象经过怎样的平移得到?
的图象经过怎样的平移得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com