
【题目】如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB.CD相交于点O,B.D两点立于地面,经测量:
AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,
tan61.9°≈0.553;可使用科学记算器)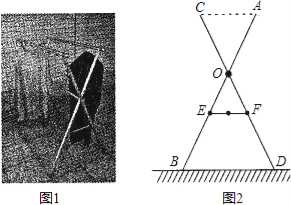
【答案】(1)见解析(2)61.9°(3)会拖落到地面,理由见解析
【解析】
(1)根据等角对等边得出∠OAC=∠OCA=![]() (180°﹣∠BOD)和∠OBD=∠ODB=
(180°﹣∠BOD)和∠OBD=∠ODB=![]() (180°﹣∠BOD),进而利用平行线的判定得出即可;
(180°﹣∠BOD),进而利用平行线的判定得出即可;
(2)首先作OM⊥EF于点M,则EM=16cm,利用cos∠OEF=![]() 0.471,即可得出∠OEF的度数;
0.471,即可得出∠OEF的度数;
(3)首先证明Rt△OEM∽Rt△ABH,进而得出AH的长即可.
(1)证明:证法一:∵AB.CD相交于点O,
∴∠AOC=∠BOD…1分
∵OA=OC,
∴∠OAC=∠OCA=![]() (180°﹣∠BOD),
(180°﹣∠BOD),
同理可证:∠OBD=∠ODB=![]() (180°﹣∠BOD),
(180°﹣∠BOD),
∴∠OAC=∠OBD,…2分
∴AC∥BD,…3分
证法二:AB=CD=136cm,OA=OC=51cm,
∴OB=OD=85cm,
∴![]()
又∵∠AOC=∠BOD
∴△AOC∽△BOD,
∴∠OAC=∠OBD;
∴AC∥BD
(2)解:在△OEF中,OE=OF=34cm,EF=32cm;
作OM⊥EF于点M,则EM=16cm;
∴cos∠OEF=![]() 0.471,
0.471,
用科学记算器求得∠OEF=61.9°;
(3)解法一:小红的连衣裙会拖落到地面;
在Rt△OEM中,![]() =30cm,
=30cm,
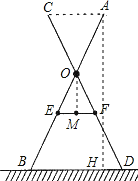
过点A作AH⊥BD于点H,
同(1)可证:EF∥BD,
∴∠ABH=∠OEM,则Rt△OEM∽Rt△ABH,
∴![]()
所以:小红的连衣裙垂挂在衣架后的总长度122cm>晒衣架的高度AH=120cm.
解法二:小红的连衣裙会拖落到地面;
同(1)可证:EF∥BD,∴∠ABD=∠OEF=61.9°;
过点A作AH⊥BD于点H,在Rt△ABH中
![]() ,
,
AH=AB×sin∠ABD=136×sin61.9°=136×0.882≈120.0cm
所以:小红的连衣裙垂挂在衣架后的总长度122cm>晒衣架的高度AH=120cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
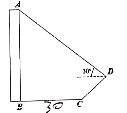
【题目】为测量大楼![]() 的高度,从距离大楼底部
的高度,从距离大楼底部![]() 30米处的
30米处的![]() ,有一条陡坡公路,车辆从
,有一条陡坡公路,车辆从![]() 沿坡度
沿坡度![]() ,坡面长13米的斜坡到达
,坡面长13米的斜坡到达![]() 后,观测到大楼的顶端
后,观测到大楼的顶端![]() 的仰角为30°,则大楼的高度为( )米.
的仰角为30°,则大楼的高度为( )米.
(精确到0.1米,![]() ,
,![]() )
)
A.26.0B.29.2C.31.1D.32.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
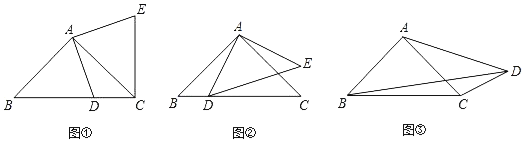
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
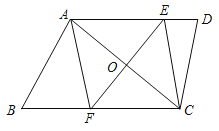
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连结AF、CE.
(1)求证:△AOE≌△COF.
(2)试判断四边形AFCE的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市高新区某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的售价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:![]() .
.
(1)工人甲第几天生产的产品数量为60件?
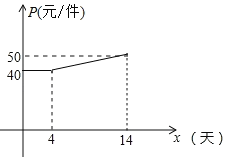
(2)设第x天生产的产品成本为P元/件,P与x的函数关系图象如图,工人甲第x天创造的利润为W元,求W与x的函数关系式,第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.若以点B为圆心,1.6为半径作圆⊙B,使点M和点N都在⊙B外,则x的取值范围是( )
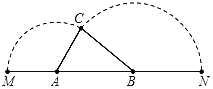
A.1<x<2B.0.6<x<1.6C.1<x<1.6D.1<x<1.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com