【题目】为测量大楼
的高度，从距离大楼底部
30米处的
，有一条陡坡公路，车辆从沿坡度
，坡面长13米的斜坡到达
后，观测到大楼的顶端
的仰角为30°，则大楼的高度为（ ）米．
（精确到0.1米，
，
）
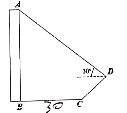
A.26.0B.29.2C.31.1D.32.2
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知点P0的坐标为（2，0），将点P0绕着原点O按逆时针方向旋转60°得点P1，延长OP1到点P2，使OP2=2OP1，再将点P2绕着原点O按逆时针方向旋转60°得点P3，则点P3的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图，根据图中提供的信息，完成以下问题：
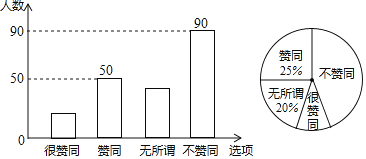
（1）本次共调查了 名家长；扇形统计图中“很赞同”所对应的圆心角是 度．已知该校共有1600名家长，则“不赞同”的家长约有 名；请补全条形统计图；
（2）从“不赞同”的五位家长中（两女三男），随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座，请用树状图或列表法求出选中“1男1女”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】参照学习函数的过程与方法，探究函数
的图象与性质列表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值为纵坐标，描出相应的点，如图所示：
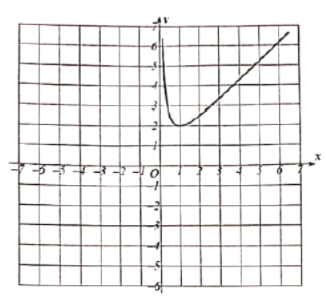
（1）请补全函数图象：
（2）观察图象并分析表格，回答下列问题：
①当
时，y随x的增大而_________；（填“增大”或“减小”）
②图象关于点__________中心对称．（填点的坐标）
③当
时，
的最小值是_________．
（3）结合函数图象，当
时，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，以
为斜边，作直角
，使点
落在内，
．
（1）如图1，若
，
，
，点
分别为
边的中点，连接
，求线段的长；
（2）如图2，若，把绕点
逆时针旋转一定角度，得到
，连接
并延长交
于点
，求证：
．
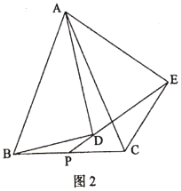
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点
是
轴上一点，其坐标为
，点
在
轴的正半轴上.点
，
均在线段
上，点的横坐标为
，点的横坐标大于，在
中，若
轴，
轴， 则称为点，的“肩三角形.
(1)若点坐标为
， 且
，则点，的“肩三角形”的面积为__ ；
(2)当点，的“肩三角形”是等腰三角形时，求点的坐标；
(3)在(2)的条件下，作过
，，三点的抛物线
.
①若
点必为抛物线上一点，求点，的“肩三角形”面积
与之间的函数关系式，并写出自变量的取值范围.
②当点，的“肩三角形”面积为3，且抛物线与点，的“肩三角形”恰有两个交点时，直接写出的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，小红家阳台上放置了一个晒衣架．如图2是晒衣架的侧面示意图，立杆AB．CD相交于点O，B．D两点立于地面，经测量：
AB=CD=136cm，OA=OC=51cm，OE=OF=34cm，现将晒衣架完全稳固张开，扣链EF成一条直线，且EF=32cm．
（1）求证：AC∥BD；
（2）求扣链EF与立杆AB的夹角∠OEF的度数（精确到0.1°）；
（3）小红的连衣裙穿在衣架后的总长度达到122cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．
（参考数据：sin61.9°≈0.882，cos61.9°≈0.471，
tan61.9°≈0.553；可使用科学记算器）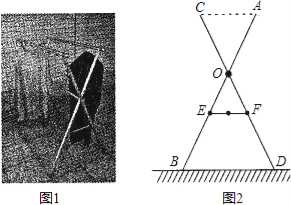
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践：
问题情境：矩形旋转中的数学
已知在矩形
中，
，
，以点
为旋转中心，逆时针旋转矩形，旋转角为
，得到矩形
，点
、点
、点
的对应点分别为点
、点
、点
．
操作猜想：
（1）如图①，当点落在
边上时，求线段
的长度；
深入探究：
（2）如图②，当点落在线段
上时，
与相交于点
，连接
，求线段
的长度；
（3）请从，两题中任选一题作答，我选______题．
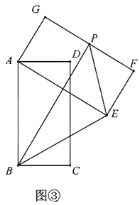
题：如图③，设点
为边
的中点，连接
，
，
，在矩形旋转过程中，
的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．
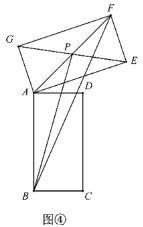
题：如图④，设点为矩形对角线交点，连接，
，在矩形旋转过程中，
的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
