【题目】如图，从水平地面看一山坡上的通讯铁塔PC，在点A处用测角仪测得塔顶端点P的仰角是45°，向前走9m到达B点，用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°．

（1）求∠BPC的度数．
（2）求该铁塔PF的高度，（结果精确到0.1m，参考数据： ．）

参考答案：

【答案】
（1）解：延长PC交直线AB于点F，交直线DE于点G，则PF⊥AF，

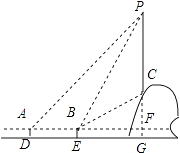
依题意得：∠PAF=45°，∠PBF=60°，∠CBF=30°

∴∠BPC=90°﹣60°=30°；


（2）解：根据题意得：AB=DE=9，FG=AD=1.3，

设PC=x m，则CB=CP=x，

在Rt△CBF中，BF=xcos30°= x，CF= x，

在Rt△APF中，FA=FP，

∴9+ x= x+x，x=9+3 ，

∴PC=9+3 ≈14.2，

∴PF= x+x=21.3．

即该铁塔PF的高度约为21.3 m


【解析】（1）根据题意用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°，根据三角形内角和定理求出∠BPC；（2）根据解直角三角形，在Rt△CBF中，求出BF=xcos30°的值，从而求出该铁塔PF的高度.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能正确解答此题．

关闭