
【题目】数学课上,同学们探究下面命题的正确性,顶角为36°的等腰三角形我们称之为黄金三角形,“黄金三角形“具有一种特性,即经过它某一顶点的一条直线可以把它分成两个小等腰三角形,为此,请你,解答问题:
(1)已知如图1:黄金三角形△ABC中,∠A=36°,直线BD平分∠ABC交AC于点D,求证:△ABD和△DBC都是等腰三角形;

(2)如图,在△ABC中,AB=AC,∠A=36°,请你设计三种不同的方法,将△ABC分割成三个等腰三角形,不要求写出画法,不要求证明,但是要标出所分得的每个三角形的各内角的度数.
(3)已知一个三角形可以被分成两个等腰三角形,若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.




【答案】(1)见解析;(2)见解析;(3)最大角的可能值为72°,90°,108°,126°,132°
【解析】
(1)通过角度转换得到∠ABD=∠BAD,和∠BDC=72°=∠C,即可判断;
(2)根据等腰三角形的两底角相等及三角形内角和定理进行解答即可;
(3)设原△ABD中有一个角为36°,可分成两个等腰三角形,逐个讨论:①当分割的直线过顶点B时②当分割三角形的直线过点D时情况和过点B一样的,③当分割三角形的直线过点A时,在分别求出最大角的度数即可.
解:(1)证明:∵∠ABC=(180-36)÷2=72;BD平分∠ABC,∠ABD=72÷2=36°,
∴∠ABD=∠BAD,
∴△ABD为等腰三角形,
∴∠BDC=72°=∠C,
∴△BCD为等腰三角形;
(2)根据等腰三角形的两底角相等及三角形内角和定理作出,如图所示:



(3)设原△ABD中有一个角为36°,可分成两个等腰三角形,逐个讨论:
①当分割的直线过顶点B时,
【1】:第一个等腰三角形ABC以A为顶点:则第二个等腰三角形BCD只可能以C为顶点
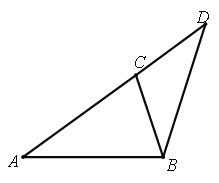
此时∠A=36°,∠D=36°,∠B=72+36=108°,最大角的值为108°;
【2】:第一个等腰三角形ABC以B为顶点:第二个等腰三角形BCD只可能以C为顶点

此时:∠A=36°,∠D=18°,∠B=108+18=126°,最大角的值为126°;
【3】第一个等腰三角形ABC以C为顶点:第二个等腰三角形BCD有三种情况
△BCD以B为顶点:∠A=36°,∠D=72°,
∴∠ABD=72°,最大角的值为72°;
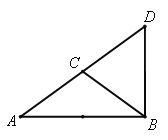
△BCD以C为顶点:∠A=36°,∠D=54°,
∴∠ABD=90°,最大角的值为90°;
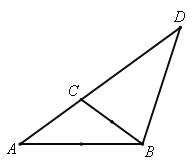
△BCD以D为顶点:∠A=36°,∠D=36°
∴∠ABD=108°,最大角的值为108°;
②当分割三角形的直线过点D时情况和过点B一样的;
③当分割三角形的直线过点A时,

此时∠A=36°,∠D=12°,∠B=132°,
最大角的值为132°;
综上所述:最大角的可能值为72°,90°,108°,126°,132°.


科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举办的“新城杯”足球联赛,新城中学七(1)班学生去商场购买了A品牌足球1个、B品牌足球2个,共花费400元,七(2)班学生购买了品牌A足球3个、B品牌足球1个,共花费450元.
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元?
(2)为了进一步发展“校园足球”,学校准备再次购进A、B两种品牌的足球,学校提供专项经费850元全部用于购买这两种品牌的足球,学校这次最多能购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为![]() 的小正方形(
的小正方形(![]() ),将余下的部分拼成一个梯形,根据两个图形中阴影部分面积关系,解决下列问题:
),将余下的部分拼成一个梯形,根据两个图形中阴影部分面积关系,解决下列问题:
(1)如图①所示,阴影部分的面积为 (写成平方差形式).

(2)如图②所示,梯形的上底是 ,下底是 ,高是 ,根据梯形面积公式可以算出面积是 (写成多项式乘法的形式).

(3)根据前面两问,可以得到公式 .
(4)运用你所得到的公式计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
课间餐种类 | 人类 | 百分比 |
鸡腿 | 150 | 60% |
薯饼 | 30 | a |
鱼丸 | b | 12% |
鸡柳 | 40 | c |
(1)样本容量是 , a= , b= , c= .
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),在x轴上截得的线段长为 ![]() .
.
(1)求a、c的值.
(2)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“贡献值”,记作g(k).求g(k)的解析式.
(3)在(2)条件下,当“贡献值”g(k)=1时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: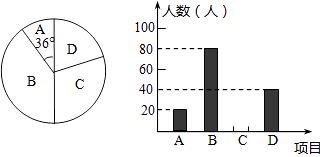
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据: ![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com