
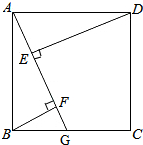
 如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.分析 (1)先利用等角的余角相等得到∠BAF=∠ADE,则可根据”AAS“判定△ABF≌△DAE,得到BF=AE,所以AF-BF=AF-AE=EF;
(2)设AE=BF=a,则AF=a+1,由(1)得△ABF≌△DAE,所以DE=AF=a+1,在Rt△ADE中利用勾股定理得到AD2=a2+(a+1)2,再证明Rt△ABF∽Rt△AGB,利用相似比得AB2=AF•AG=(a+1)×$\frac{25}{4}$,所以a2+(a+1)2=(a+1)×$\frac{25}{4}$,整理得8a2-17a-21=0,解得a1=3,a2=-$\frac{7}{8}$(舍去),即可得到AB=5,然后利用四边形DEGC的面积=S正方形ABCD-S△ABG-S△AED进行计算.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵E⊥AG于点E,BF⊥AG于点F,
∴∠AED=∠BFA=90°,
∴∠DAE+∠ADE=90°,
而∠DAE+∠BAF=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
$\left\{\begin{array}{l}{∠AFB=∠DEA}\\{∠BAF=∠DAE}\\{AB=DA}\end{array}\right.$,
∴△ABF≌△DAE,
∴BF=AE,
∴AF-BF=AF-AE=EF;
(2)解:设AE=BF=a,则AF=a+1,
∵△ABF≌△DAE,
∴DE=AF=a+1,
在Rt△ADE中,AD2=a2+(a+1)2,
∵∠BAF=∠GAB,
∴Rt△ABF∽Rt△AGB,
∴AB:AG=AF:AB,
∴AB2=AF•AG=(a+1)×$\frac{25}{4}$,
而AB=AD,
∴a2+(a+1)2=(a+1)×$\frac{25}{4}$,
整理得8a2-17a-21=0,解得a1=3,a2=-$\frac{7}{8}$(舍去),
∴AB=$\sqrt{(3+1)×\frac{25}{4}}$=5,
∴四边形DEGC的面积=S正方形ABCD-S△ABG-S△AED
=5×5-$\frac{1}{2}$×3×$\frac{25}{4}$-$\frac{1}{2}$×3×4
=$\frac{77}{8}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质和三角形全等的判定与性质.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5y2-2y2=3 | B. | x6+x2=x8 | C. | (-a-b)2=a2-2ab+b2 | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
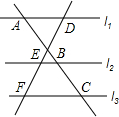 如图所示,已知:l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{m}{n}$,试说明:$\frac{DE}{DF}$=$\frac{m}{m+n}$.
如图所示,已知:l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{m}{n}$,试说明:$\frac{DE}{DF}$=$\frac{m}{m+n}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批电视机的使用寿命 | B. | 了解全国六年级学生的视力情况 | ||
| C. | 了解渤海湾中鱼的种类 | D. | 了解你们班上的同学每周上网情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com