
分析 ①分母有理化即可;
②利用已知等式得原式=$\sqrt{2}$-1+$\sqrt{3}$$-\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$,然后合并即可.
解答 解:①原式=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$
=$\sqrt{n+1}$-$\sqrt{n}$;
②原式=$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$
=$\sqrt{2}$-1+$\sqrt{3}$$-\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$
=$\sqrt{100}$-1
=10-1
=9.
故答案为$\sqrt{n+1}$-$\sqrt{n}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


科目:初中数学 来源: 题型:解答题
斐波那契(约1170-1250)是意大利数学家,他研究了一列数, 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到 的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的 瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质, 在实际生活中也有广泛的应用. 斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$ 表示(其中n≥1),这是用无理数表示有理数的一个范例. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
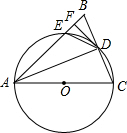 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
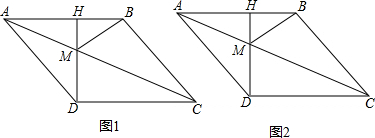
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com