
【题目】如图,在边长为1的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() .
.
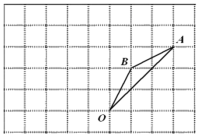
(1)画出![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
(2)求在旋转过程中,点![]() 经过的路径的长;
经过的路径的长;
(3)求在旋转过程中,线段![]() 所扫过的面积.
所扫过的面积.
科目:初中数学 来源: 题型:
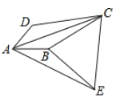
【题目】如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.
(1)求证:△ADC≌△ABE;
(2)求证:![]()
(3)若AB=2,点Q在四边形ABCD内部运动,且满足![]() ,直接写出点Q运动路径的长度.
,直接写出点Q运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
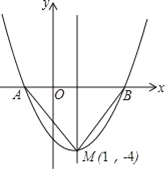
【题目】如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=![]() S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x+3.
(1)求函数图象的顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y>0时,自变量x的取值范围;
②当2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE、BE是△ABC的两个内角的平分线,过点A作AD⊥AE.交BE的延长线于点D.若AD=AB,BE:ED=1:2,则cos∠ABC=_____.
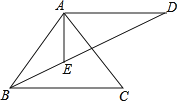
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com