
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
【答案】(1)甲、乙工程队每天能完成绿化的面积分别是![]() 、
、![]() ;(2)
;(2)![]() ;(3)安排甲队施工
;(3)安排甲队施工![]() 天,乙队施工
天,乙队施工![]() 天,施工总费用最低,最低费用为
天,施工总费用最低,最低费用为![]() 万元.
万元.
【解析】
(1)设乙工程队每天能完成绿化的面积是![]() m2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
m2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
(2)根据题意得到100x+50y=2400,整理得:y=-2x+48,即可解答;
(3)根据甲乙两队施工的总天数不超过30天,得到x≥18,设施工总费用为w元,根据题意得:![]() ,根据一次函数的性质,即可解答.
,根据一次函数的性质,即可解答.
(1)设乙工程队每天能完成绿化面积是![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,
是原方程的解,
则甲工程队每天能完成绿化的面积是![]()
答:甲、乙工程队每天能完成绿化的面积分别是![]() 、
、![]() ;
;
(2)根据题意得:![]() ,
,
整理得:![]() ,
,
∴y与x的函数解析式为:![]() .
.
(3)∵甲乙两队施工的总天数不超过30天,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
设施工总费用为![]() 元,根据题意得:
元,根据题意得:
![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() 万元,
万元,
此时,![]() ,
,
答:安排甲队施工![]() 天,乙队施工
天,乙队施工![]() 天,施工总费用最低,最低费用为
天,施工总费用最低,最低费用为![]() 万元.
万元.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() .
.
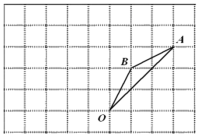
(1)画出![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
(2)求在旋转过程中,点![]() 经过的路径的长;
经过的路径的长;
(3)求在旋转过程中,线段![]() 所扫过的面积.
所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O直径AB=12cm,AM和BN是⊙O的切线,DC切⊙O于点E且交AM于点D,交BN于点C,设AD=x,BC=y.
(1)求y与x之间的关系式;
(2)x,y是关于t的一元二次方程2t2﹣30t+m=0的两个根,求x,y的值;
(3)在(2)的条件下,求△COD的面积.
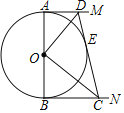
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
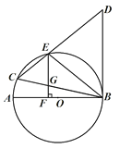
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1.
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k的值和AC12+(kDD1)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
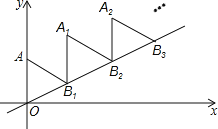
【题目】如图,放置的△OAB1,△B1A1B2,△B2A2B3,都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3都在直线y=![]() x上,则点A2019的坐标为__________________
x上,则点A2019的坐标为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
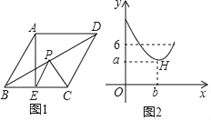
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段![]() 和
和![]() 的端点
的端点![]() 均在格点上.
均在格点上.
(1)在图中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在格点上,使
在格点上,使![]() 的面积为4,且
的面积为4,且![]() 的一个角的正切值是
的一个角的正切值是![]() ;
;
(2)在图中画出以![]() 为顶角的等腰
为顶角的等腰![]() (非直角三角形),点
(非直角三角形),点![]() 在格点上.请你直接写出
在格点上.请你直接写出![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践空及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
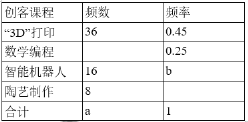

请根据图表中提供的信息回答下列问题
(1)統计表中的a= ,b= ;
(2)“陶艺制作”对应扇形的圆心角为 ;
(3)学校为开设这四门课程,需要对参加“3D”打印课程每个人投资200元,预计A、B、C、D四门课程每人投资比为4:3:6:5,求学校开设创客课程需为学生人均投资多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com