
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践空及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
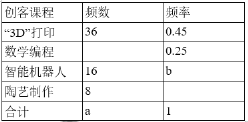

请根据图表中提供的信息回答下列问题
(1)統计表中的a= ,b= ;
(2)“陶艺制作”对应扇形的圆心角为 ;
(3)学校为开设这四门课程,需要对参加“3D”打印课程每个人投资200元,预计A、B、C、D四门课程每人投资比为4:3:6:5,求学校开设创客课程需为学生人均投资多少钱?
【答案】(1)80,0.2;(2)36°;(3)212.5元
【解析】
(1)根据“3D”打印的频数和频率可以求得a的值,然后根据b对应的频数即可求得b的值;
(2)根据频数分布表中的数据可以求得“陶艺制作”对应扇形的圆心角的度数;
(3)根据题意和题目中的数据,可以求得学校为开设创客课程,需为学生人均投入多少钱.
解:(1)a=36÷0.45=80,
b=16÷80=0.2,
故答案为:80,0.2;
(2)“陶艺制作”对应扇形的圆心角为:360°×![]() =36°,
=36°,
故答案为:36°;
(3)∵每生A、B、C、D四科投资比为4:3:6:5,“3D打印课程每人投资200元,
∴每生A、B、C、D四科投资分别为:200元、150元、300元、250元,![]() (200×36)+150×(80×0.25)+300×16+250×8=212.5(元),
(200×36)+150×(80×0.25)+300×16+250×8=212.5(元),
即学校为开设创客课程,需为学生人均投入212.5元.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 在
在![]() 和
和![]() 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数![]() 的图象与二次函数的图象都经过点A
的图象与二次函数的图象都经过点A![]() ,求m和k的值;
,求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移![]() 个单位后得到的图象记为C,同时将(2)中得到的直线
个单位后得到的图象记为C,同时将(2)中得到的直线![]() 向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
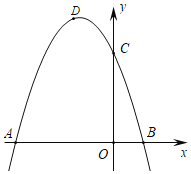
【题目】如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3)点D为抛物线的顶点.
(1)求抛物线C1的解析式;
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在请求出点F的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
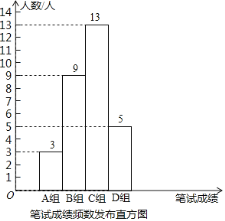
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
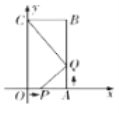
【题目】如图,四边形OABC是矩形,点A坐标为(2,0),点C坐标为(0,4).点P从点O出发,沿OA以每秒1个单位长度的速度向点A运动,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当△CBQ与△PAQ相似时,求出t的值;
(2)当t=1时,抛物线y=2x2+bx+c经过P,Q两点,与y轴交于点M,在该抛物线上找点D,使∠MQD=![]() ∠MPQ,求点D的坐标.
∠MPQ,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )

A.2B.4C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com