
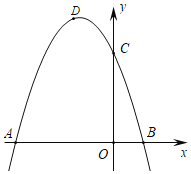
【题目】如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3)点D为抛物线的顶点.
(1)求抛物线C1的解析式;
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在请求出点F的坐标,若不存在请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)存在,当点F为(3,﹣4+2![]() )或(3,﹣4﹣2
)或(3,﹣4﹣2![]() )或(3,4)或(3,﹣
)或(3,4)或(3,﹣![]() )时,使得△BEF为等腰三角形
)时,使得△BEF为等腰三角形
【解析】
(1)将A、B、C三点代入一般式,即可求出解析式;
(2)由折叠的性质和旋转的性质可求抛物线C2解析式和抛物线C3解析式,可得点E坐标,由等腰三角形的性质可求点F坐标.
解:(1)设解析式y=a(x﹣1)(x+3)
将C(0,3)代入得 a=﹣1
∴抛物线C1的解析式为y=﹣x2﹣2x+3;
(2)∵抛物线C1的解析式为y=﹣x2﹣2x+3;
∴抛物线C1的顶点为(﹣1,4)
∵将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,
∴抛物线C2解析式为:y=﹣(x﹣3)2+4,抛物线C3解析式为:y=(x﹣3)2﹣4,
∵点E为抛物线C3的顶点,
∴点E(3,﹣4),
∴BE=![]() ,
,
∵点F抛物线C2的对称轴上,
∴点F横坐标为3,
若BE=EF=2![]() ,则点F坐标为(3,﹣4+2
,则点F坐标为(3,﹣4+2![]() )或(3,﹣4﹣2
)或(3,﹣4﹣2![]() ),
),
若BE=BF时,则点F与点E关于x轴对称,
∴点F(3,4),
若BF=EF时,则22+(4﹣EF)2=BF2,
∴BF=EF=![]() ,
,
∴点F(3,﹣![]() ),
),
综上所述:当点F为(3,﹣4+2![]() )或(3,﹣4﹣2
)或(3,﹣4﹣2![]() )或(3,4)或(3,﹣
)或(3,4)或(3,﹣![]() )时,使得△BEF为等腰三角形
)时,使得△BEF为等腰三角形


科目:初中数学 来源: 题型:
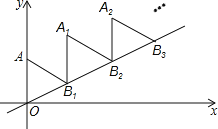
【题目】如图,放置的△OAB1,△B1A1B2,△B2A2B3,都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3都在直线y=![]() x上,则点A2019的坐标为__________________
x上,则点A2019的坐标为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕业典礼的开幕式上需要采购花店的鲜花.花店提供甲、乙两种造型的花束数量若干,甲种花束由4枝红花、1枝黄花和1枝紫花搭配而成,乙种花束由4枝黄花和2枝紫花搭配而成.已知每枝红花、黄花和紫花的成本之比是3:2:1,甲、乙两种造型的花束数量之比是2:9.甲、乙两种花束成本价分别为每种造型的三种鲜花的成本之和,甲种花束的销售利润率是20%,乙种花束的销售利润率为10%,这次买卖,花店获得的利润率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践空及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
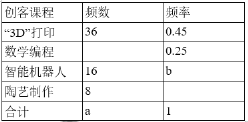

请根据图表中提供的信息回答下列问题
(1)統计表中的a= ,b= ;
(2)“陶艺制作”对应扇形的圆心角为 ;
(3)学校为开设这四门课程,需要对参加“3D”打印课程每个人投资200元,预计A、B、C、D四门课程每人投资比为4:3:6:5,求学校开设创客课程需为学生人均投资多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
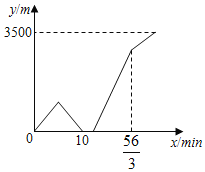
【题目】5月的第二个周日是母亲节,丁丁精心地设计了一份手工礼物送给妈妈.为了尽快完成手工礼物,丁丁骑自行车到位于家正东方向的商店购买材料.丁丁离家5分钟后自行车出现故障,丁丁立即打电话通知在家看报纸的爸爸带上工具箱来帮忙维修(丁丁打电话和爸爸找工具箱的时间忽略不计),同时丁丁以原来一半的速度推着自行车继续走向商店.爸爸接到电话后,立刻出发追赶丁丁,追上丁丁后,爸爸用2分钟的时间修好了自行车,并立刻以原速到位于家正西方500米的公司上班(爸爸换电话的时间忽略不计),丁丁则以原来的骑车速度到达商店.在整个过程中,丁丁和爸爸保持匀速行驶.如图是丁丁、爸爸的距离y(米)与丁丁的出发时间x(分钟)之间的函数图象,则爸爸到达公司时,丁丁距离商店_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第15秒时,点P的坐标是( )
个单位长度,则第15秒时,点P的坐标是( )
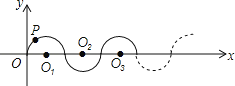
A.(15,1)B.(15,﹣1)C.(30,1)D.(30,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,经过点(-1,0),有下列结论:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正确的结论有( )
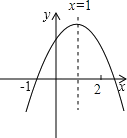
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
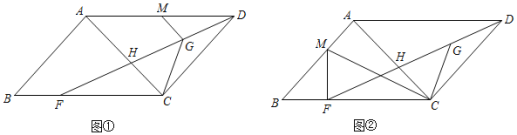
【题目】如图,ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2![]() ,求GM;
,求GM;
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com