
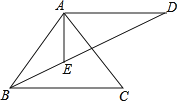
【题目】如图,AE、BE是△ABC的两个内角的平分线,过点A作AD⊥AE.交BE的延长线于点D.若AD=AB,BE:ED=1:2,则cos∠ABC=_____.
【答案】![]()
【解析】
取DE的中点F,连接AF,根据直角三角形斜边中点的性质得出AF=EF,然后证得△BAF≌△DAE,得出AE=AF,从而证得△AEF是等边三角形,进一步证得∠ABC=60°,即可求得结论.
取DE的中点F,连接AF,
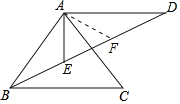
∴EF=DF,
∵BE:ED=1:2,
∴BE=EF=DF,
∴BF=DE,
∵AB=AD,
∴∠ABD=∠D,
∵AD⊥AE,EF=DF,
∴AF=EF,
在△BAF和△DAE中
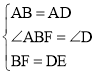
∴△BAF≌△DAE(SAS),
∴AE=AF,
∴△AEF是等边三角形,
∴∠AED=60°,
∴∠D=30°,
∵∠ABC=2∠ABD,∠ABD=∠D,
∴∠ABC=60°,
∴cos∠ABC=cos60°=![]() ,
,
故答案为:![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
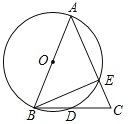
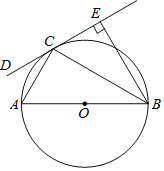
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧![]() 是劣弧
是劣弧![]() 的2倍;⑤AE=BC,其中正确的序号是_________.
的2倍;⑤AE=BC,其中正确的序号是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() ,
,![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() .
.
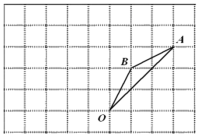
(1)画出![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
(2)求在旋转过程中,点![]() 经过的路径的长;
经过的路径的长;
(3)求在旋转过程中,线段![]() 所扫过的面积.
所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3张相同的纸牌,它们分别标有数字3,﹣1,2,随机摸出一张纸牌不放回,记录其标有的数字为x,再随机摸取一张纸牌,记录其标有的数字为y,这样就确定点P的一个坐标为(x,y)
(1)用列表或画树状图的方法写出点P的所有可能坐标;
(2)写出点P落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC,BC.
(1)求证:BC平分∠ABE;
(2)若⊙O的半径为3,cosA=![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
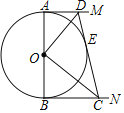
【题目】⊙O直径AB=12cm,AM和BN是⊙O的切线,DC切⊙O于点E且交AM于点D,交BN于点C,设AD=x,BC=y.
(1)求y与x之间的关系式;
(2)x,y是关于t的一元二次方程2t2﹣30t+m=0的两个根,求x,y的值;
(3)在(2)的条件下,求△COD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
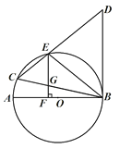
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段![]() 和
和![]() 的端点
的端点![]() 均在格点上.
均在格点上.
(1)在图中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在格点上,使
在格点上,使![]() 的面积为4,且
的面积为4,且![]() 的一个角的正切值是
的一个角的正切值是![]() ;
;
(2)在图中画出以![]() 为顶角的等腰
为顶角的等腰![]() (非直角三角形),点
(非直角三角形),点![]() 在格点上.请你直接写出
在格点上.请你直接写出![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com