【题目】如图，在
中，
，
，
，
，
，点
在
上，
交
于点
，
交
于点
，当
时，
________．
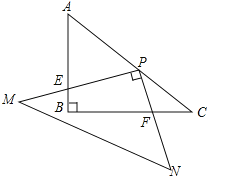
【答案】3
【解析】
如图作PQ⊥AB于Q，PR⊥BC于R．由△QPE∽△RPF，推出
=
=2，可得PQ=2PR=2BQ，由PQ∥BC，可得AQ：QP：AP=AB：BC：AC=3：4：5，设PQ=4x，则AQ=3x，AP=5x，BQ=2x，可得2x+3x=3，求出x即可解决问题．
如图，作PQ⊥AB于Q，PR⊥BC于R．
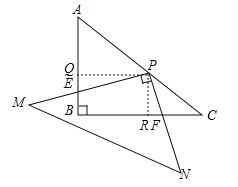
∵∠PQB=∠QBR=∠BRP=90°，∴四边形PQBR是矩形，∴∠QPR=90°=∠MPN，∴∠QPE=∠RPF，∴△QPE∽△RPF，∴==2，∴PQ=2PR=2BQ．
∵PQ∥BC，∴AQ：QP：AP=AB：BC：AC=3：4：5，设PQ=4x，则AQ=3x，AP=5x，BQ=2x，∴2x+3x=3，∴x=
，∴AP=5x=3．
故答案为：3．
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2＋bx＋c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y＝kx＋1(k≠0)的图象上，它的对称轴是x＝1.有下列四个结论，①. abc＜0； ②. a＜－
；③. a＝－k；④. 当0＜x＜1时，ax＋b＞k，其中正确结论的个数是( )
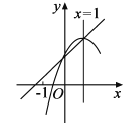
A.1；B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于C点，且对称轴为x＝1，点B坐标为（﹣1，0），则下面的四个结论，其中正确的个数为（ ）
①2a+b＝0②4a﹣2b+c＜0③ac＞0④当y＞0时，﹣1＜x＜4
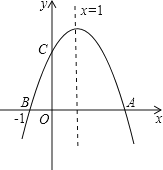
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．
（1）求点A、B、C的坐标；
（2）设动点N（－2，n），求使MN＋BN的值最小时n的值；
（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似，（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（
，
为常数）.
（1）当
，
时，求二次函数的最小值；
（2）当
时，若在函数值
的情况下，只有一个自变量
的值与其对应，求此时二次函数的解析式；
（3）当
时，若在自变量的值满足≤≤
的情况下，与其对应的函数值
的最小值为21，求此时二次函数的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
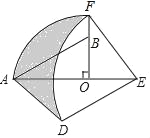
【题目】如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
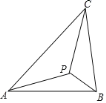
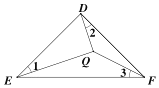
【题目】如图所示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点，三角形的布洛卡点是法国数学家长数学教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名.问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=______________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
