
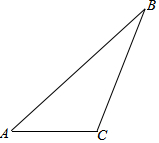
 如图,在△ABC中,先按如下步骤尺规作图再计算:
如图,在△ABC中,先按如下步骤尺规作图再计算:分析 (1)∠BAC的平分线AD如图所示.
(2)线段AD的垂直平分线MN,分别交AB、AC于点E、F,如图所示.
(3)首先证明四边形AEDF是菱形,推出AE=DE=AF=DF=4,由DE∥AC,推出$\frac{BE}{EA}$=$\frac{BD}{DC}$,由此即可解决问题.
解答 解:(1)∠BAC的平分线AD如图所示.
(2)线段AD的垂直平分线MN,分别交AB、AC于点E、F,如图所示.
(3)∵EA=ED,FA=FD,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵∠EAD=∠FAD,
∴∠EDA=∠FAD,∠EAD=∠FDA,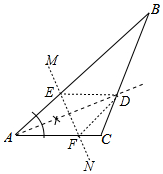
∴DE∥AF,AE∥DF,
∴四边形AEDF是平行四边形,∵EA=ED,
∴四边形AEDF是菱形,
∴AE=DE=AF=DF=4,
∵DE∥AC,
∴$\frac{BE}{EA}$=$\frac{BD}{DC}$,
∴$\frac{BE}{4}$=$\frac{6}{3}$,
∴BE=8.
点评 本题考查复杂作图、线段的垂直平分线的性质、菱形的判定和性质、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b<0 | D. | a<0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
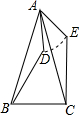 如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.
如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | (-$\sqrt{3}$)0 | C. | (-$\frac{2}{3}$)-2 | D. | |-2| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com