
����Ŀ��ijУΪ�˽���꼶ѧ�����÷�������������ȡ���꼶����ѧ����������ij���ڿ����Ϸ��ԵĴ���������ͳ�ƣ��������±�������������ͼ��ʾ��������������ͳ��ͼ����֪![]() ��
��![]() ���鷢�������ı�Ϊ
���鷢�������ı�Ϊ![]() ������ͼ��������ݻش��������⣺
������ͼ��������ݻش��������⣺
���Դ��� | |
|
|
|
|
|
|
|
|
|
|
|
|
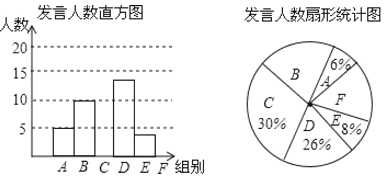
��1�������������������ȫֱ��ͼ��
��2�����꼶����ѧ��1500�ˣ������ȫ�꼶��������Դ���������12�ε�������
��3����֪![]() �鷢�Ե�ѧ����ǡ��1λ������
�鷢�Ե�ѧ����ǡ��1λ������![]() �鷢�Ե�ѧ������2λŮ�����ִ�
�鷢�Ե�ѧ������2λŮ�����ִ�![]() ����
����![]() ���зֱ��һλѧ��д���棬�����б�������״ͼ�ķ��������������λѧ��ǡ����һ��һŮ�ĸ���
���зֱ��һλѧ��д���棬�����б�������״ͼ�ķ��������������λѧ��ǡ����һ��һŮ�ĸ���
���𰸡���1��50��ֱ��ͼ����������2��ȫ�꼶��������Դ���������12�ε�����Ϊ270�ˣ���3��![]()
��������
��1������B�������������E��������Ȼ����E����������E���������ڵİٷֱȼ����������������Ȼ�����C��������F�����������ȫֱ��ͼ���ɣ�
��2�����E��F����������ռ�İٷֱȵĺ��ٳ�1500����������ۣ�
��3�������A��������Ȼ��������⣬������״ͼ��Ȼ�����ø��ʹ�ʽ���㼴�ɣ�
�⣺��1��E������Ϊ10��5��2=4���ˣ�
��������Ϊ4��8%=50
C������Ϊ50��30%=15���ˣ�
B��������ռ�ٷֱ�Ϊ10��50=20%
��F��������ռ�ٷֱ�Ϊ1��6%��20%��30%��26%��8%=10%
��F�������Ϊ50��10%=5���ˣ�
��ȫֱ��ͼ���£�

��2��E��F����������ռ�İٷֱȵĺ�Ϊ8%��10%=18%
1500��18%=270���ˣ�
��ȫ�꼶��������Դ���������12�ε�����Ϊ270�ˣ�
��3��A������Ϊ50��6%=3���ˣ�
����״ͼ����
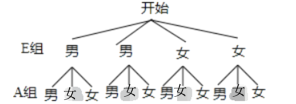
����12�ֵȿ��ܵĽ�����������λѧ��ǡ����һ��һŮ�Ľ������6��
���������λѧ��ǡ����һ��һŮ�ĸ���Ϊ6��12=![]()


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
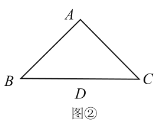
��1����ͼ�٣�����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ����̽��
����̽��![]() ��
��![]() ��������ϵ����˵���ı���
��������ϵ����˵���ı���![]() ������Ƕ�ֵ�����ǣ�������������ǣ���˵�����ɣ�
������Ƕ�ֵ�����ǣ�������������ǣ���˵�����ɣ�
��2������![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ӳ����ϵĵ㣬��
�ӳ����ϵĵ㣬��![]() ����ô
����ô![]() ��������ͼ��˵�����ɣ�
��������ͼ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ���Ҷ�����
���Ҷ�����![]() ���ϣ���
���ϣ���![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() �������Ϊ
�������Ϊ![]() ����
����![]() �������ߵĶԳ����ϣ�ֱ��
�������ߵĶԳ����ϣ�ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
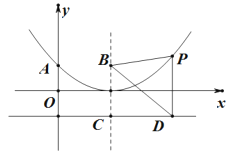
��1����������ߵĺ�������ʽ��
��2����![]() �ǣ�1����ͼ���ϵĵ㣬����
�ǣ�1����ͼ���ϵĵ㣬����![]() ��
��![]() ��Ĵ�����ֱ��
��Ĵ�����ֱ��![]() ���ڵ�
���ڵ�![]() �����ж�
�����ж�![]() �Ƿ�Ϊ���������Σ���˵�����ɣ�
�Ƿ�Ϊ���������Σ���˵�����ɣ�
��3����![]() �ڵ�
�ڵ�![]() ������
������![]() �Ӻ�����2013���˶���������2019��ʱ���������
�Ӻ�����2013���˶���������2019��ʱ���������![]() �˶���·������
�˶���·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC������ֱ�ߣ������̶ȣ�����Բ�棬������Ҫ����ͼ����Ҫ��д��������Ҫ������ͼ�ۼ�����
��1��������AMNP��ʹ��M��N��P�ڱ�AB��BC��CA�ϣ�
��2������A=60�㣬AB=8��AC=6ʱ��������AMNP�������
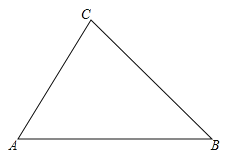
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ��һ�㣮�������
��һ�㣮�������![]() ����һ��
����һ��![]() ����
����![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ȫ�ȣ������Ǽס������˵�������
ȫ�ȣ������Ǽס������˵�������
���ף�����![]() ����
����![]() ���д��߷ֱ�
���д��߷ֱ�![]() ��
��![]() ��
��![]() �㡢
�㡢![]() �㣬��
�㣬��![]() ��
��![]() ���㼴Ϊ����
���㼴Ϊ����
���ң���![]() ����
����![]() ƽ�е�ֱ�߽�
ƽ�е�ֱ�߽�![]() ��
��![]() �㣬��
�㣬��![]() ����
����![]() ƽ�е�ֱ�߽�
ƽ�е�ֱ�߽�![]() ��
��![]() �㣬��
�㣬��![]() ��
��![]() ���㼴Ϊ����
���㼴Ϊ����
���ڼס������˵������������жϺ�����ȷ����������

A. ���˽���ȷB. ���˽Դ���
C. ����ȷ���Ҵ���D. �״�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У������²�����ͼ���ٷֱ��Ե�C�͵�DΪԲ�ģ�����![]() Ϊ�뾶�������������ڵ�M��N������ֱ��MN����
Ϊ�뾶�������������ڵ�M��N������ֱ��MN����![]() ǡ�þ�����A����CD���ڵ�E������BE��������˵��������ǣ� ��
ǡ�þ�����A����CD���ڵ�E������BE��������˵��������ǣ� ��
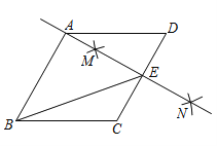
A.![]() B.
B.![]() C.��AB=4����
C.��AB=4����![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����14�֣���ͼ1����ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������B���߶�AE�ϣ���C���߶�AD�ϣ�
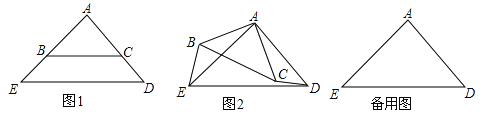
��1����ֱ��д���߶�BE���߶�CD�Ĺ�ϵ�� ��
��2����ͼ2����ͼ1�е���ABC�Ƶ�A˳ʱ����ת������0������360������
����1���еĽ����Ƿ��������������������ͼ2֤����������������˵�����ɣ�
����AC=![]() EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�ǡ�O��һ�㣬OA��AB����OA=1��AB=![]() ��OB����O�ڵ�D����AC��OB������ΪM��������O�ڵ�C������BC��
��OB����O�ڵ�D����AC��OB������ΪM��������O�ڵ�C������BC��
��1����֤��BC�ǡ�O�����ߣ�
��2������B��BP��OB����OA���ӳ����ڵ�P������PD����sin��BPD��ֵ��
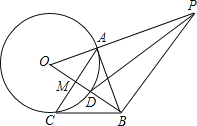
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B���������ֱ�Ϊ(8��0)��(0��8)����C��F�ֱ���ֱ��x����5��x���ϵĶ��㣬CF��10����D���߶�CF���е㣬����AD��y���ڵ�E�����ABE��������ֵΪ_____��
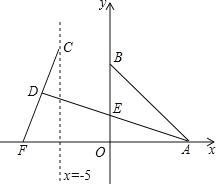
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com