
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
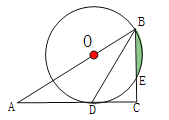
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,由BD为角平分线得到一对角相等,再根据等腰三角形的性质得出一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直角,即可得证;
(2)过O作OG垂直于BE,可得出四边形ODCG为矩形,利用勾股定理求出BG的长,根据相似三角形的性质即可得到结论.
(1)证明:连接OD,如图,∵BD为∠ABC平分线,∴∠1=∠2.
∵OB=OD,∴∠1=∠3,∴∠2=∠3,∴OD∥BC.
∵∠C=90°,∴∠ODA=90°,∴AC是⊙O的切线;
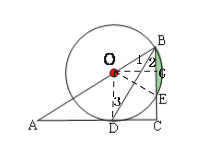
(2)过O作OG⊥BC,连接OE,则四边形ODCG为矩形,∴GC=OD=OB=10,OG=CD=![]() .在Rt△OBG中,利用勾股定理得:BG=5,∴BE=10,则△OBE是等边三角形,∴阴影部分面积为
.在Rt△OBG中,利用勾股定理得:BG=5,∴BE=10,则△OBE是等边三角形,∴阴影部分面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
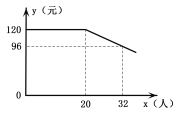
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程
与x轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程![]() 无实数根;③
无实数根;③![]() ≥0.其中,正确结论的个数为( )
≥0.其中,正确结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
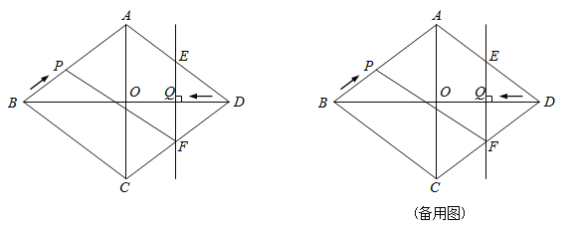
【题目】已知:如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE∶S菱形ABCD=17∶40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
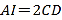
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com