
【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.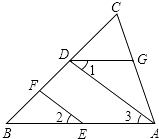
解:因为EF∥AD,
所以∠2=().
又因为∠1=∠2,
所以∠1=∠3().
所以AB∥().
所以∠BAC+=180°().
因为∠BAC=80°,
所以∠AGD= .
【答案】∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;∠AGD=180°;两直线平行,同旁内角互补;100°.
【解析】解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等);
又∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补),
∵∠BAC=80°,
∴∠AGD=100°.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.
(1)把﹣16,9,16,﹣5,﹣9,5分别填入图中的六个小正方形中;
(2)若某相对两个面上的数字分别为 ![]() 和
和 ![]() ﹣5,求x的值.
﹣5,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=( ) 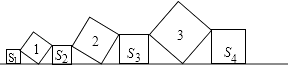
A.5
B.4
C.6
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
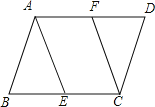
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.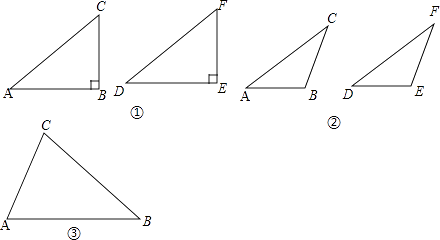
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 , 可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 , 则△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏为了解我市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
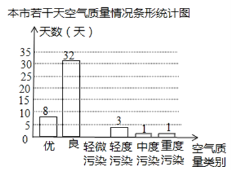
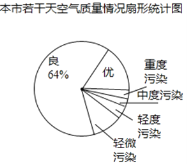
请你根据图中提供的信息,解答下列问题:
(1)计算被抽取的天数;
(2)请补全条形统计图,并求扇形统计图中表示优的扇形的圆心角度数;
(3)请估计该市这一年(365天)达到优和良的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
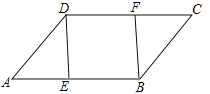
【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com