
【题目】小敏为了解我市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
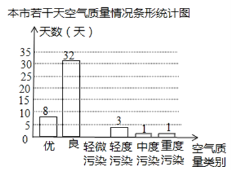
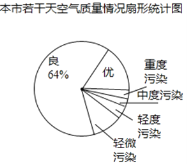
请你根据图中提供的信息,解答下列问题:
(1)计算被抽取的天数;
(2)请补全条形统计图,并求扇形统计图中表示优的扇形的圆心角度数;
(3)请估计该市这一年(365天)达到优和良的总天数.
【答案】(1)50;(2)补全图形见解析,57.6°;(3)292.
【解析】
试题分析:(1)根据扇形图中空气为良所占比例为64%,条形图中空气为良的天数为32天,即可得出被抽取的总天数;
(2)利用轻微污染天数是50-32-8-3-1-1=5天;表示优的圆心角度数是![]() ×360°=57.6°,即可得出答案;
×360°=57.6°,即可得出答案;
(3)利用样本中优和良的天数所占比例得出一年(365天)达到优和良的总天数即可.
试题解析:(1)∵扇形图中空气为良所占比例为64%,条形图中空气为良的天数为32天,
∴被抽取的总天数为:32÷64%=50(天);
(2)轻微污染天数是50-32-8-3-1-1=5天;
表示优的圆心角度数是![]() ×360°=57.6°,
×360°=57.6°,
如图所示:
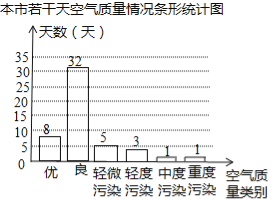
(3)∵样本中优和良的天数分别为:8,32,
∴一年(365天)达到优和良的总天数为:![]() ×365=292(天).
×365=292(天).
∴估计该市一年达到优和良的总天数为292天.
考点: 1.条形统计图;2.用样本估计总体;3.扇形统计图.


科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.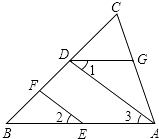
解:因为EF∥AD,
所以∠2=().
又因为∠1=∠2,
所以∠1=∠3().
所以AB∥().
所以∠BAC+=180°().
因为∠BAC=80°,
所以∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数x、y、z满足x2+y2+z2=4,则(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是( )
A.12
B.20
C.28
D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是 . 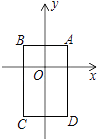
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC , D为边BC上一点,以AB、BD为邻边作平行四边形ABDE , 连接AD、EC . 若BD=CD , 求证:四边形ADCE是矩形.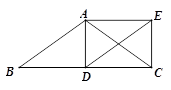
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AD上一点,射线OC,射线OB,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.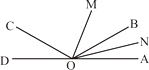
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com