练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果(3m＋3n＋2)(3m＋3n－2)＝77，那么m＋n的值为________．

    【答案】±3

    【解析】

    把原式变形后用平方差公式展开得到（m＋n）2，进而得到m+n的值.

    原式=[(3m＋3n)+2][ (3m＋3n)-2]= (3m＋3n)2-22= (3m＋3n)2-4=77，

    得(3m＋3n)2=81，

    即3m+3n=±9，

    m+n=±3，

    故答案为：±3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

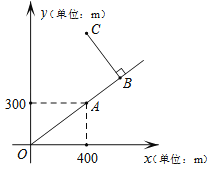
    【题目】如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向左转90°后直行400m到达梅花阁C，则点C的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

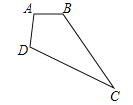
    【题目】如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．

    （1）若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．

    （2）若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O，OM⊥AB，NO⊥CD，∠1= ∠BOC．

    （1）求∠1的大小；
    （2）求∠BON的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，EF∥AD，∠1=∠2，∠BAC=80°．将求∠AGD的过程填写完整．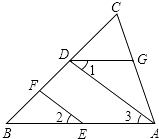

    解：因为EF∥AD，
    所以∠2=（）．
    又因为∠1=∠2，
    所以∠1=∠3（）．
    所以AB∥（）．
    所以∠BAC+=180°（）．
    因为∠BAC=80°，
    所以∠AGD= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD沿BD对折，点A落在E处，BE与CD相交于F，若AD=3，BD=6．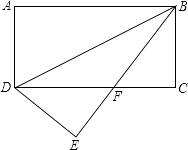
    （1）求证：△EDF≌△CBF；
    （2）求∠EBC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知(x2+px+8)(x2-3x+q)的展开式中不含x2，x3项，求p、q的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知实数x、y、z满足x2+y2+z2=4，则（2x﹣y）2+（2y﹣z）2+（2z﹣x）2的最大值是（　　）
    A.12
    B.20
    C.28
    D.36

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某职业高中机电班共有学生42人，其中男生人数比女生人数的2倍少3人．

    （1）该班男生和女生各有多少人？

    （2）某工厂决定到该班招录30名学生，经测试，该班男、女生每天能加工的零件数分别为50个和45个，为保证他们每天加工的零件总数不少于1460个，那么至少要招录多少名男学生？

    查看答案和解析>>

    同步练习册答案