
 如图,点A,O,D三点在一条直线上,∠AOB=20°,∠BOC=3∠COD.
如图,点A,O,D三点在一条直线上,∠AOB=20°,∠BOC=3∠COD.分析 (1)先求得∠BOD=160°,然后根据∠BOC=3∠COD,可求得∠COD=40°;
(2)设运动时间x秒,根据∠BOC=40°,列方程求解即可;
(3)OP的位置分两种,设∠POC=x,根据角之间的关系列出方程,求方程即可得出结论.
解答 解:(1)∵∠BOC=3∠COD,∠AOB=20°,∠AOB+∠BOC+∠COD=180°,
∴4∠COD=180°-20°,
∴∠COD=40°,
故答案为:40°.
(2)设运动时间为t,则∠BOC=|120°-(30°+10°)×t|,
∵射线OB,OC旋转的角度都不超过180°,
∴t≤$\frac{180°}{30°}$=6秒,
令∠BOC=40°,即|120°-40°×t|=40°,
解得t1=2,t2=4.
故运动2秒和4秒时,∠BOC=40°.
(3)按照题意画图,如下,

设∠POC=x,
∵∠AOC+∠BOC=20°,∠DOB+∠BOD=40°,
∴∠BOD-∠AOC=20°①,
∵∠BOD-∠AOP=3∠POC=3x②,
②-①得:
$\left\{\begin{array}{l}{x=3x-20°(OP在∠AOC内)}\\{-x=3x-20°(OP在∠COB内)}\end{array}\right.$,
解得:x=10°,x=5°.
答:此时∠POC的度数5°或者15°.
点评 本题考查了角的运算,解题的关键是理清角与角之间的关系,列对关系式.


科目:初中数学 来源: 题型:填空题
 如图,正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是2π-4≤x≤$\frac{16}{3}$π-4$\sqrt{3}$.
如图,正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是2π-4≤x≤$\frac{16}{3}$π-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
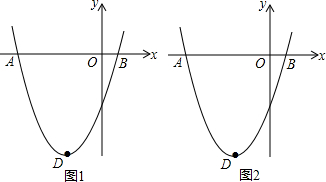
 如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(3,-16).
如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(3,-16).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$.
如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1,旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM=6-$\frac{12\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC与△ABD中,AD与BC相交于点O.∠1=∠2,请你添加一个条件(不再添加其他线段相等,不标注或使用其他字母),使OC=OD,并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于点O.∠1=∠2,请你添加一个条件(不再添加其他线段相等,不标注或使用其他字母),使OC=OD,并给出证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com