Question

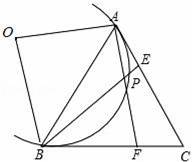
等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．

（1）若AE=CF；

①求证：AF=BE，并求∠APB的度数；

②若AE=2，试求AP•AF的值；

（2）若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长．

　

　

Answer 1

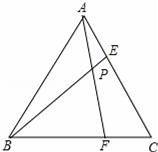
【考点】相似三角形的判定与性质；全等三角形的判定与性质；等边三角形的性质．

【专题】证明题；压轴题；动点型．

【分析】（1）①证明△ABE≌△CAF，借用外角即可以得到答案；②利用勾股定理求得AF的长度，再用平行线分线段成比例定理或者三角形相似定理求得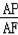的比值，即可以得到答案．

（2）当点F靠近点C的时候点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP为等腰三角形，继而求得半径和对应的圆心角的度数，求得答案．点F靠近点B时，点P的路径就是过点B向AC做的垂线段的长度；

【解答】（1）①证明：∵△ABC为等边三角形，

∴AB=AC，∠C=∠CAB=60°，

又∵AE=CF，

在△ABE和△CAF中，

，

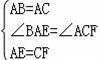
∴△ABE≌△CAF（SAS），

∴AF=BE，∠ABE=∠CAF．

又∵∠APE=∠BPF=∠ABP+∠BAP，

∴∠APE=∠BAP+∠CAF=60°．

∴∠APB=180°﹣∠APE=120°．

②∵∠C=∠APE=60°，∠PAE=∠CAF，∴△APE∽△ACF，

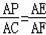
∴，即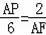，所以AP•AF=12

 

（2）若AF=BE，有AE=BF或AE=CF两种情况．

①当AE=CF时，点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP为等腰三角形，且∠ABP=∠BAP=30°，

∴∠AOB=120°，

又∵AB=6，

∴OA=，

点P的路径是．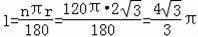

②当AE=BF时，点P的路径就是过点C向AB作的垂线段的长度；因为等边三角形ABC的边长为6，所以点P的路径为：．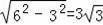

所以，点P经过的路径长为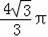或3．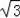

【点评】本题考查了等边三角形性质的综合应用以及相似三角形的判定及性质的应用，解答本题的关键是注意转化思想的运用．