
| A. | 0 | B. | 1 | C. | $\frac{2016}{2015}$ | D. | 2015 |
分析 根据题意依次计算出第1、2、3次运算后的结果,观察到结果中分母是序数加1、分子始终为1、另一个因数均为2016,以此规律可得操作2015次后所得的结果.
解答 解:根据题意,第1次运算的结果为:2016-$\frac{1}{2}$×2016=$\frac{1}{2}$×2016;
第2次运算的结果为:$\frac{1}{2}$×2016-$\frac{1}{2}$×2016×$\frac{1}{3}$=$\frac{1}{2}$×2016×$\frac{2}{3}$=$\frac{1}{3}$×2016;
第3次运算的结果为:$\frac{1}{3}$×2016-$\frac{1}{3}$×2016×$\frac{1}{4}$═$\frac{1}{3}$×2016×$\frac{3}{4}$=$\frac{1}{4}$×2016;
…
故第2015次运算的结果为:$\frac{1}{2016}$×2016=1,
故选:B.
点评 本题主要考查从变化的数字中总结规律并加以应用的能力,从已知数的变化中观察变化的部分是如何变化及弄清不变的部分是总结规律的关键,一般将变化的部分与序数相联系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | (-2,-a) | B. | (2,a) | C. | (2,-a) | D. | (a,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
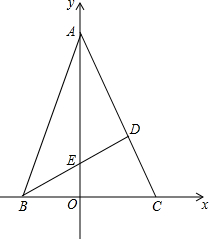 如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒
如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com