
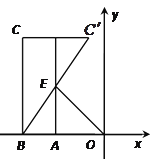
【题目】如图, 已知点A的坐标为(m,0)点B的坐标为(![]() ,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,
,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C, ![]() 关于直线
关于直线![]() 对称,
对称, ![]() 交直线
交直线![]() 于点E若△BOE的面积为4,则点E的坐标为_______.
于点E若△BOE的面积为4,则点E的坐标为_______.
【答案】(4,4)或![]()
【解析】先根据矩形的性质与轴对称的性质得出AB=C′D,再利用AAS证明△ABE≌△DC′E,得出AE=DE=﹣m.根据△BOE的面积为4,列出方程(2﹣m)(﹣m)=4,解方程即可.
如图,设AE与CC′交于点D.
∵点A的坐标为(m,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO, ∴CB=﹣2m.
∵点C,C′关于直线x=m对称,
∴CD=C′D,
∵ABCD是矩形,AB=CD,
∴AB=C′D.
又∵∠BAE=∠C′DE=90°,∠AEB=DEC′,
∴△ABE≌△DC′E,
∴AE=DE,
∴AE=AD=BC=﹣m.
∵△BOE的面积为4,
∴(2﹣m)(﹣m)=4,
整理得,m2﹣2m﹣8=0,
解得m=4或﹣2,
∵在x轴上方取点C,
∴﹣2m>0,
∴m<0,
∴m=4不合题意舍去,
“点睛”本题考查了矩形的性质,轴对称的性质,全等三角形的与性质,三角形的面积,得出AE=DE=﹣m是解题关键.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )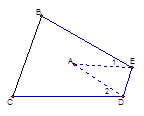
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长BC与宽AB的关系是( ) 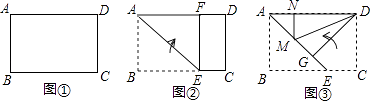
A.BC=2AB
B.BC= ![]() AB
AB
C.BC=1.5AB
D.BC= ![]() AB
AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( ) 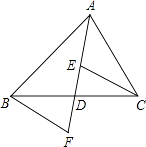
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年合肥市共有30293名考生参加中考,为了了解这30293名考生的数学成绩,从中抽取了1000名生的数学成绩进行统计分析,以下说法中,错误的是( )
A. 这种调查采用了抽样调查的方式
B. 30293名考生是总体
C. 从中抽取的1000名学生的数学成绩是总体的一个样本
D. 样本容量是1000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对2.07801分别取近似值,其中错误的是( )
A. 2.1(精确到0.1) B. 2.08(精确到千分位)
C. 2.08(精确到百分位) D. 2.0780(精确到0.0001)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com