
【题目】制造厂的某车间生产圆形铁片和长方形铁片,如图,两个圆形铁片和一个长方形铁片可以制造成一个油桶.已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.问安排生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?

科目:初中数学 来源: 题型:
【题目】为了考查一种零件的加工精度,从中抽出40只进行检测,其尺寸数据如下(单位:微米):
161,165,164,166,160,158,163,162,168,159,
147,165,167,151,164,159,152,159,149,172,
162,157,162,169,156,164,163,157,163,165,
173,159,157,169,165,154,153,163,168,169.
试列出样本频数及频率分布表,绘制频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=105°,在BC,CD上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM的度数为 ( )

A. 100° B. 105° C. 120° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
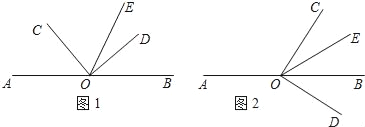
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
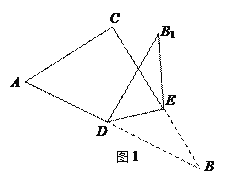
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
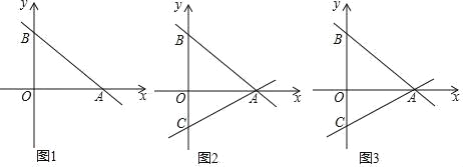
【题目】如图1,平面直角坐标系中,直线AB:y=﹣![]() x+b交x轴于点A(8,0),交y轴正半轴于点B.
x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)求抛物线的解析式;
(2)用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;
(3)求△BCE的面积最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com