Question

15．某农庄计划在30亩空地上全部种植蔬菜和水果，菜农小张和果农小李分别承包了种植蔬菜和水果的任务，小张种植每亩蔬菜的工资y（元）与种植面积m（亩）之间的函数关系如图①所示，小李种植水果所得报酬z（元）与种植面积n（亩）之间的函数关系如图②所示
（1）如果种植蔬菜20亩，则小张种植每亩蔬菜的工资是140元，小张应得的工资总额是2800元，此时，小李种植水果10亩，小李应得的报酬是1500元；
（2）设农庄支付给小张和小李的总费用为W（元），当10＜m＜30时，求W与m之间的函数关系式，并求出总费用最大为多少？

Answer 1

分析 （1）根据图象数据解答即可；
（2）设z=kn+b（k≠0），然后利用待定系数法求一次函数解析式即可；
（3）先求出20＜m≤30时y与m的函数关系式，再分①10＜m≤20时，10＜n≤20；②20＜m≤30时，0＜n≤10两种情况，根据总费用等于两人的费用之和列式整理即可得解．

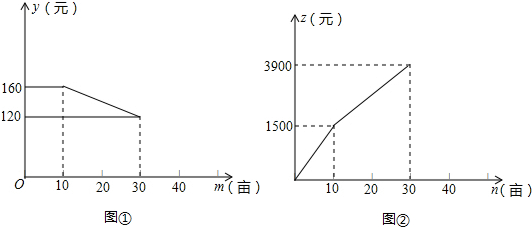
解答 解：（1）由图可知，如果种植蔬菜20亩，则小张种植每亩蔬菜的工资是$\frac{1}{2}$（160+120）=140元，
小张应得的工资总额是：140×20=2800元，
此时，小李种植水果：30-20=10亩，
小李应得的报酬是1500元；
故答案为：140；2800；10；1500；

（2）当10＜n≤30时，设z=kn+b（k≠0），
∵函数图象经过点（10，1500），（30，3900），
∴$\left\{\begin{array}{l}{10k+b=1500}\\{30k+b=3900}\end{array}\right.$，
解得 $\left\{\begin{array}{l}{k=120}\\{b=300}\end{array}\right.$，
所以，z=120n+300（10＜n≤30）；

（3）当10＜m≤30时，设y=km+b，
∵函数图象经过点（10，160），（30，120），
∴$\left\{\begin{array}{l}{10k+b=160}\\{30k+b=120}\end{array}\right.$，
解得 $\left\{\begin{array}{l}{k=-2}\\{b=180}\end{array}\right.$，
∴y=-2m+180，
∵m+n=30，
∴n=30-m，
∴①当10＜m≤20时，10≤n＜20，
w=m（-2m+180）+120n+300，
=m（-2m+180）+120（30-m）+300，
=-2m²+60m+3900，
②当20＜m≤30时，0＜n≤10，
w=m（-2m+180）+150n，
=m（-2m+180）+150（30-m），
=-2m²+30m+4500，
所以，w与m之间的函数关系式为w=$\left\{\begin{array}{l}{-2{m}^{2}+60m+3900（10＜m≤20）}\\{-2{m}^{2}+30m+4500（20＜m≤30）}\end{array}\right.$．
∵w=-2m²+60m+3900=-2（x-15）²+4350；
w=-2m²+30m+4500=-2（x-$\frac{15}{2}$）²+4612.5，
∴w的最大值为4612.5（元）．
∴总费用最大为4612.5元．

点评 本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，（3）难点在于要分情况讨论并注意m、n的取值范围的对应关系，这也是本题最容易出错的地方．