
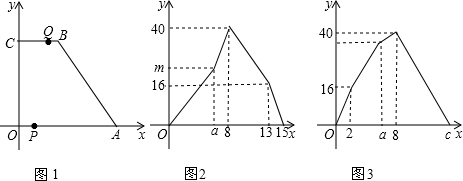
分析 第(1)小题,通过观察图1可以看出,要使四边形PABC为平行四边形,需满足AP∥BC,且AP=BC,进而求出OP的长度,根据时间=路程÷速度,即可求出a;观察图2,可以看出m是当时间是6s时△OPC的面积,根据面积公式,求出m即可;根据时间是8s时,△OPC的面积为40,即可求得点P的运动速度b;根据点Q改变速度后运动的距离和时间,即求得d;通过观察图3可知,c表示点Q从点C出发到点O所用的时间,可根据点Q从点A运动到点O,运动的距离为10,速度是1cm/s,求出时间即可;
第(2)小题,根据题意,作出辅助线,过点O作OM⊥AB于点M,根据三角形全等,求得AM=AN,求出BM的长度,即求得点Q从点C运动到点M的距离,从而求出点Q的运动时间;根据△AQP∽△ABO,求出∠AQP=∠AB0,进而证明QP∥BO,即可证明四边形OPQB为等腰梯形;
第(3)小题,根据点P、Q在6s后改变了速度,用改变速度前运动的路程+改变速度后运动的路程即可表示出点P离开点O的路程y1(cm)与出发后的运动时间x(s)的函数关系式;用总的路程-点Q运动的路程,即可表示出点Q距O的路程y2(cm)与出发后的运动时间x(s)的函数关系式;点P、Q两点相遇,即y1=y2,即可求得相遇时的时间;
(4)根据距离不大于18,可得|y2-y1|≤18,解不等式组即可.
解答 解:(1)要使四边形PABC为平行四边形,需满足AP∥BC,且AP=BC,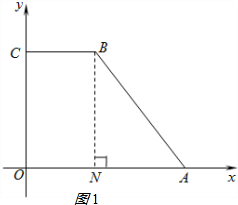
∵A(10,0),B(4,8),C(0,8),
∴BC=4cm,
∴OP=OA-AP=10-4=6cm,
∴a=6÷1=6s.
此时,${S}_{△OPC}=\frac{1}{2}×6×8=24,m=24c{m}^{2}$,
8s时,${S}_{△OPC}=\frac{1}{2}(6+2b)×8=40$,
∴b=2cm/s.
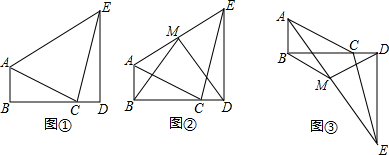
如图1,过点B作BN⊥OA于点N,在△BMA中,BN=8cm,ON=BC=4cm,
∴AN=10-4=6cm,
∴$AB=\sqrt{A{N}^{2}+B{N}^{2}}=\sqrt{{6}^{2}+{8}^{2}}=10$cm,
当点P运动6s时,点Q运动到距离点A是2cm的位置,当时间为8s时,△OPC和△OQC的面积相等,即点P和点Q重合,
∴点Q改变速度后,2s运动的距离为2cm,
∴2d=2,d=1cm/s,
d(c-8)=10,c=18s.
(2)如图2,过点O作OM⊥AB于点M;连接PQ.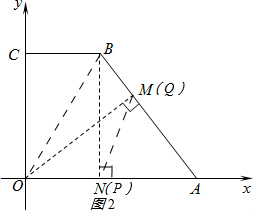
在△BNA和△OAM中,$\left\{\begin{array}{l}{∠BNA=∠OMA=90°}\\{∠BAN=∠OAM}\\{AB=OA}\end{array}\right.$,
∴△BNA≌△OAM(AAS),
∴AM=AN=6cm,
∴BM=AB-AM=10-6=4cm,
c当点Q运动到点M处时,OQ⊥AB,点Q运动的路程为:BC+BM=4+4=8cm,
∴点Q运动的时间为:8÷2=4s,
∴当Q运动4s时,OQ⊥AB.
当点Q运动4s时,点P运动4s,则点P运动到点N处,
在△AQP和△ABO中,$\frac{AQ}{AB}=\frac{AP}{AO}$且∠QAP=∠BAO,
∴△AQP∽△ABO,
∴∠AQP=∠AB0,
∴QP∥BO.
又BQ=OP=4cm,
∴四边形OPQB为等腰梯形.
(3)由(1)可以,点P、Q运动6s后改变速度,
∴点P离开点O的路程为:y1=6+2(x-6)=2x-6;
点Q距离点O的距离为:y2=24-[12+(x-6)]=18-x,
点P、Q相遇时,y1=y2,即2x-6=18-x,解得:x=8s.
(4)根据题意,得|y2-y1|≤18,
即-18≤18-x-(2x-6)≤18,
解不等式组,得2≤x≤14.
点评 本题主要考查了特殊四边形、全等三角形、相似三角形及不等式组的综合运用,熟练掌握知识点是解决综合题目的关键;能够读懂3个图是解决此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
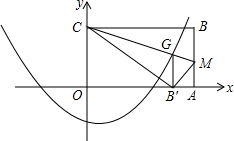 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com