
分析 (1)根据平方和负整数指数幂的计算法则计算即可求解;
(2)仿照(1)计算即可作出判断;
(3)根据(1)(2)得出发现;
(4)根据负整数指数幂的计算法则计算即可求解.
解答 解:(1)我们发现($\frac{2}{3}$)2=($\frac{3}{2}$)-2;
故答案为:=;
(2)∵$(\frac{5}{4})^{3}$=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$=$\frac{125}{64}$,
$(\frac{4}{5})^{-3}$=$\frac{1}{(\frac{4}{5})^{3}}$=$\frac{1}{\frac{4}{5}}$×$\frac{1}{\frac{4}{5}}$×$\frac{1}{\frac{4}{5}}$=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$=$\frac{125}{64}$
∴$(\frac{5}{4})^{3}$=$(\frac{4}{5})^{-3}$.
(3)我们可以发现:($\frac{b}{a}$)-m=$(\frac{a}{b})^{m}$(ab≠0).
故答案为:=;
(4)($\frac{7}{15}$)-2=($\frac{15}{7}$)2=$\frac{225}{49}$.
点评 考查了负整数指数幂,负整数指数幂:a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数),注意:①a≠0;②计算负整数指数幂时,一定要根据负整数指数幂的意义计算,避免出现(-3)-2=(-3)×(-2)的错误.③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.④在混合运算中,始终要注意运算的顺序.


科目:初中数学 来源: 题型:解答题
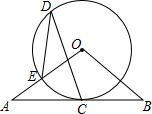 如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.
如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
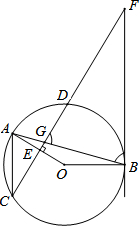 如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.
如图,在⊙0中,弦AB与弦CD交于点G,OA⊥CD于E,过点B的直线与CD的延长线交于点F,AC∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.
如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com