
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
| 2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则2t-3=0 | t=$\frac{3}{2}$ | t=$\frac{3}{2}>0$ | $\sqrt{x}$=$\frac{3}{2}$,所以x=$\frac{9}{4}$ |
| x+2$\sqrt{x}$-3=0 | 令$\sqrt{x}$=t,则t2+2t-3=0 | t=-3或t=1 | t=-3<0,t=1>0 | $\sqrt{x}$=1,所以x=1 |
| x+$\sqrt{x-2}-4=0$ | 令$\sqrt{x-2}$=t,则t2+t-2=0 | t=-2或t=1 | t=-2<0,t=1>0 | $\sqrt{x-2}$=1,所以x=3 |
分析 令$\sqrt{x}$=t,则t2+2t-3=0,求出t的值,再进行检验;令$\sqrt{x-2}$=t,则t2+t-2=0,求出t的值,再进行检验,最后求出x的值即可.
解答 解:②设$\sqrt{x}$=t(t≥0).则方程即可变形为t2+2t-3=0,
∴(t+3)(t-1)=0,
∴t+3=0或t-1=0,
解得,t=-3(不合题意,舍去),或t=1;
∴$\sqrt{x}$=1,
∴x=1;
③设$\sqrt{x-2}$=t.则方程即可变形为t2+t-2=0,
∴(t+2)(t-1)=0,
∴t+2=0或t-1=0,
解得,t=-2(不合题意,舍去),或t=1;
∴$\sqrt{x-2}$=1,
∴x=3;
故答案为:令$\sqrt{x}$=t,则t2+2t-3=0、t=-3或t=1、t=-3<0,t=1>0、$\sqrt{x}$=1,所以x=1;
令$\sqrt{x-2}$=t,则t2+t-2=0、t=-2或t=1、t=-2<0,t=1>0、$\sqrt{x-2}$=1,所以x=3.
点评 本题考查了解无理方程和解有理方程,关键是能把无理方程转化成有理方程,注意:解无理方程一定要进行检验.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
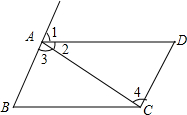 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
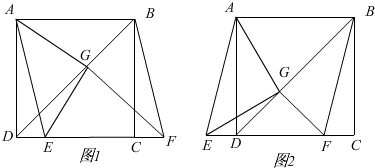
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
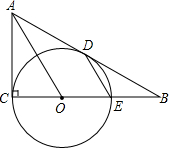 如图,在△ABC中,∠C=90°,点O在CB上,⊙O经过点C,且与AB相切于点D,与CB的另一个交点为E.
如图,在△ABC中,∠C=90°,点O在CB上,⊙O经过点C,且与AB相切于点D,与CB的另一个交点为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com