
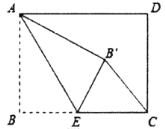
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,当
处,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为( )
的长为( )
A. 3B. ![]() C. 2或3D. 3或
C. 2或3D. 3或![]()
【答案】D
【解析】
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示。
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=![]()
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A. B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=53=2,
设BE=x,则EB′=x,CE=4x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4x)2,解得x=![]() ,
,
∴BE=![]() ;
;
②当点B′落在AD边上时,如答图2所示。
此时ABEB′为正方形,
∴BE=AB=3.
综上所述,BE的长为![]() 或3.
或3.
故选:D.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE于E点.
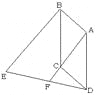
(1)求证:EF=DF;
(2)若AC=2CF,∠ADC=60 o, AC⊥DC,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某网约车公司的专车计价规则.
计费项目 | 起租价 | 里程费 | 时长费 | 远途费 |
单价 | 15元 | 2.5元/公里 | 1.5元/分 | 1元/公里 |
注:车费由起租价、里程费、时长费、远途费四部分构成,其中起租价15元含10分钟时长费和5公里里程费,远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收1元.
(1)若小李乘坐专车,行车里程为20公里,行车时间为30分,则需付车费_______元.
(2)若小李乘坐专车,行车里程为![]() 公里,平均时速为
公里,平均时速为![]() ,则小李应付车费多少元? (用含
,则小李应付车费多少元? (用含![]() 的代数式表示)
的代数式表示)
(3)小李与小王各自乘坐专车,行车车费之和为76元,里程之和为15公里(其中小王的行车里程不超过5公里).如果行驶时间均为 20分钟,那么这两辆专车此次的行驶路程各为多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等腰直角三角形,![]() ,
,![]() ,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时
,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时![]() ,
,![]() 成立.
成立.

(1)当△ABC绕点A逆时针旋转![]() 时,如图②,
时,如图②,![]() 成立吗?若成立,请证明;若不成立,请说明理由;
成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(i)求证:![]() ;
;
(ii)当![]() ,
,![]() 时,则线段FC的长为_______.
时,则线段FC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
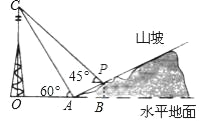
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在![]() 中,若
中,若![]() ,则
,则![]() 是“和谐三角形”.
是“和谐三角形”.

(1)等边三角形一定是“和谐三角形”,是______命题(填“真”或“假”).
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() .
.
(3)如图2,在等边三角形![]() 的边
的边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的高,若
的高,若![]() 是“和谐三角形”,且
是“和谐三角形”,且![]() .
.

①求证:![]() .
.
②连结![]() ,若
,若![]() ,那么线段
,那么线段![]() ,
,![]() ,
,![]() 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
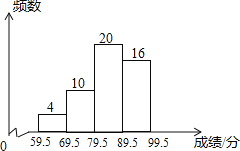
【题目】为增强学生环保意识,某中学组织全校3000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如下统计图.
请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第二组(69.5~79.5)”的扇形的圆心角 度;
(2)若成绩在90分以上(含90分)的同学可获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com