
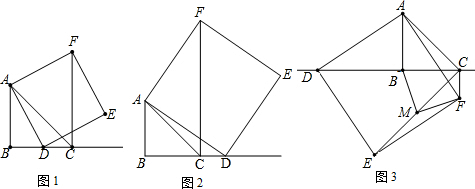
分析 (1)当点D在线段BC上时,CF、BC、BD三条线段之间的关系为:CF=BC+BD.首先根据全等三角形判定的方法,判断出△ABD≌△FGA,即可推得AB=FG,且∠AGF=90°;然后判断出四边形BCFG是矩形,即可推得CF=BG=AB+AG,再根据AB=BC,AG=BD,推得CF=BC+BD即可.
(2)首先,延长CB至G使BG=BC,连接AG,然后证明△GAD≌△CAF,据此可判断出∠BCA+∠ACF=90°,即可推得BD⊥CF.
(3)首先根据全等三角形判定的方法,判断出△ABD≌△DHE,即可推得AB=DH,BD=HE;然后判断出△EHC是等腰直角三角形,再根据全等三角形判定的方法,判断出△ADH≌△FAB,即可推得AH=BF,∠AHD=∠FBA;再判断出△BAH≌△CBF,即可推得HB=CF,∠BCF=∠ABH=90°,∠FCM=45°;最后根据全等三角形判定的方法,判断出△BHM≌△FCM,即可推得BM=FM.
解答 (1)解:CF、BC、BD三条线段之间的关系为:CF=BC+BD.
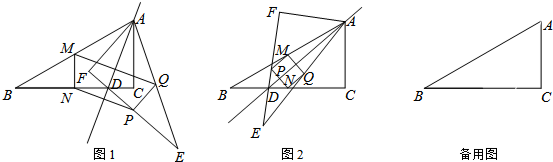
如图1,延长BA至G,使AG=BD,连接FG,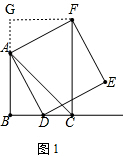
∵∠ABC=90°,
∴∠BAD+∠BDA=90°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠BAD+∠GAF=90°,
∴∠BDA=∠GAF,
在△ABD和△FGA中,
$\left\{\begin{array}{l}{BD=GA}\\{∠BDA=∠GAF}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△FGA,
∴AB=FG,且∠AGF=90°,
又∵AB=BC,
∴BC=FG,FG⊥BG,
又∵BC⊥BG,
∴FG∥BC,
∴四边形BCFG是矩形,
∴CF=BG=AB+AG,
又∵AB=BC,AG=BD,
∴CF=BC+BD.
(2)证明:如图2所示,延长CB至G使BG=BC,连接AG,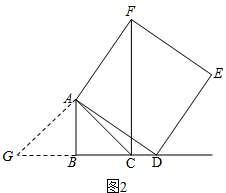
∵∠ABC=90°,BG=BC,AB=BC,
∴AG=AC,∠G=∠ACB=45°,∠GAC=90°,
∴∠GAD=∠GAC+∠CAD,∠CAF=∠CAD+∠DAF,
∴∠GAD=∠CAF,
在△GAD和△CAF中,
$\left\{\begin{array}{l}{AG=AC}\\{∠GAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△GAD≌△CAF,
∴∠ACF=∠G=45°,
∴∠BCF=∠BCA+∠ACF=90°,
∴BD⊥CF.
(3)证明:如图3,作EH⊥BD于点H,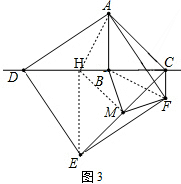
∵EH⊥BD,
∴∠EHD=90°,
∴∠EDH+∠DEH=90°,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∴∠ADB+∠EDH=90°,
∴∠ADB=∠DEH,
在△ABD和△DHE中,
$\left\{\begin{array}{l}{∠ADB=∠DEH}\\{∠ABD=∠DHE}\\{AD=DE}\end{array}\right.$,
∴△ABD≌△DHE,
∴AB=DH,BD=HE,
又∵AB=BC,
∴BC=DH,
∴CH=BD,
又∵BD=HE,
∴CH=HE,
∴△EHC是等腰直角三角形,
∴∠HCE=∠HEC=45°,
又∵M是CE的中点,
∴HM⊥CE,且HM=CM=EM,
∴∠HMC=90°,∠CHM=90°-45°=45°.
∵∠ADH+∠DAB=90°,∠FAB+∠DAB=90°,
∴∠ADH=∠FAB,
在△ADH和△FAB中,
$\left\{\begin{array}{l}{AD=FA}\\{∠ADH=∠FAB}\\{DH=AB}\end{array}\right.$,
∴△ADH≌△FAB,
∴AH=BF,∠AHD=∠FBA,
∴∠BAH+∠ABH=∠CBF+∠ABC,
∴∠BAH=∠CBF,
在△BAH和△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BAH=∠CBF}\\{AH=BF}\end{array}\right.$,
∴△BAH≌△CBF,
∴HB=CF,∠BCF=∠ABH=90°,
∴∠FCM=90°-45°=45°,
在△BHM和△FCM中,
$\left\{\begin{array}{l}{HB=CF}\\{∠BHM=∠FCM}\\{HM=CM}\end{array}\right.$,
∴△BHM≌△FCM,
∴BM=FM.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了空间想象的能力的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了直角三角形的性质和应用,要熟练掌握.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
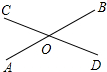 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
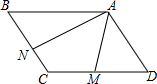 如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$.
如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com