
分析 (1)本题涉及绝对值、二次根式化简两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)本题涉及二次根式化简、三次根式化简两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)|$\sqrt{3}$-$\sqrt{5}$|+$\sqrt{(\sqrt{5}-\sqrt{7})^{2}}$
=$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$
=$\sqrt{7}$-$\sqrt{3}$;
(2)-$\sqrt{36}$+$\sqrt{2\frac{1}{4}}$-$\root{3}{-27}$
=-6+$\frac{3}{2}$+3
=$-\frac{3}{2}$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握二次根式、三次根式、绝对值等考点的运算.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
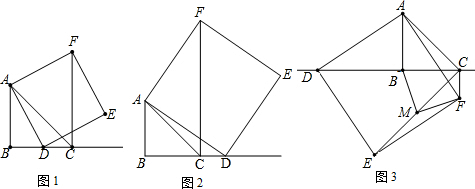
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-y)2=x2-xy+y2 | B. | -x(x2-x+1)=-x3-x2-x | ||
| C. | (2ab2)3=6a3b6 | D. | 9x3y2÷(-3x3y)=-3y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
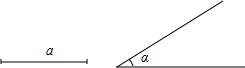 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)
已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com